Vector Fields in Orientation Space

Vector Fields in Orientation Space edit page

Vector fields in orientation space model orientation dependent spin as it occurs for instance in the Taylor or Sachs model. Another typical example are gradients of orientation distribution functions.

Orientation Dependent Spin Tensors as Vector Fields

According to Taylor theory the strain acting on a crystal with orientation ori is compensated by the action of different slip systems. The antisymmetric portion of deformation tensors of these active slip systems gives a spin tensors that describes the local misorientation the crystal undergoes under deformation. In MTEX the spin tensor W as a function of the orientation ori is computed as a variable of type SO3VectorField by the command calcTaylor.

% consider bcc symmetry and slip systems
cs = crystalSymmetry('432');
sS = slipSystem.bcc(cs)

% consider plane stain
q = 0;
epsilon = strainTensor(diag([1 -q -(1-q)]))

% compute the orientation depended spin tensor
[~,~,W] = calcTaylor(epsilon,sS.symmetrise)

sS = slipSystem (432)
 size: 1 x 3
 
   u    v    w  | h    k    l CRSS
   1   -1    1    0    1    1    1
  -1    1    1    2    1    1    1
  -1    1    1    3    2    1    1
 
epsilon = strainTensor (xyz)
  type: Lagrange 
  rank: 2 (3 x 3)
 
  1  0  0
  0  0  0
  0  0 -1
 
W = SO3VectorFieldHarmonic (432 → xyz)
  bandwidth: 32
  tangent space: rightSpinTensor

Lets visualize the spin tensor in Euler angle sections

sP = phi1Sections(cs,specimenSymmetry('222'));
sP.phi1 = (10:20:70)*degree;

% plot the Taylor factor
plot(W,sP,'resolution',7.5*degree,'layout',[2 2])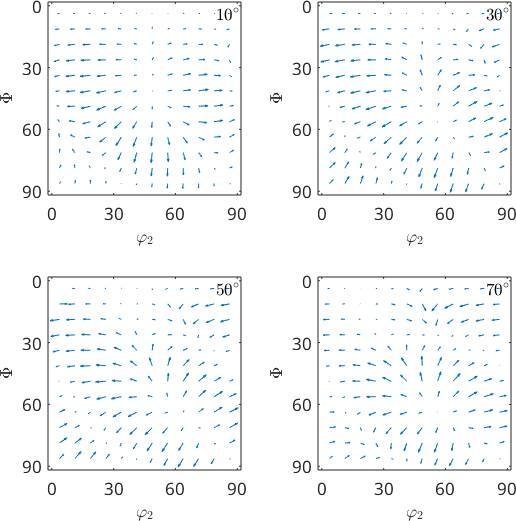

We observe how according to the orientation the Taylor model predicts a misorientation of the corresponding crystal. For a specific (set of) orientation ori we can retrieve the spin tensor by evaluating the vector field W at this position

% the spin tensor for the copper orientation
WCopper = W.eval(orientation.copper(cs))

WCopper = spinTensor (432)
  rank: 2 (3 x 3)
 
 *10^-2
       0  -4.211  20.763
   4.211       0  -16.83
 -20.763   16.83       0

The Norm of a Vector Field

The norm of the spin tensor directly relates to the amount of misorientation. We may compute the amount of misorientations as a function of orientation by the command norm and determine the orientation of maximum misorientation by

% determine the orientation of maximum misorientation
[~,oriMax] = max(norm(W))

% visualize the amount of misorientation
plot(norm(W),sP,'resolution',0.5*degree,'layout',[2 2])
mtexColorMap LaboTeX

% plot the vector field on top
hold on
plot(W,sP,'resolution',7.5*degree,'color','black')
hold off

annotate(oriMax)

oriMax = orientation (432 → xyz)
 
  Bunge Euler angles in degree
    phi1     Phi    phi2
  342.24 40.3371 43.6907

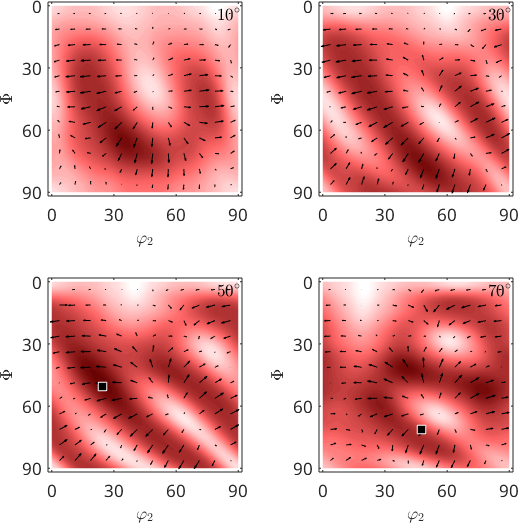
As the vector field W corresponds to the rotational axis of the local misorientation we may check how much this axis corresponds with a predefined axis, e.g. [100], by computing the inner product dot(W,d) between the vector field W and the predefined axis d.

plot(dot(W,Miller(1,0,0,cs)),sP,'layout',[2 2])
mtexColorMap blue2red
mtexColorbar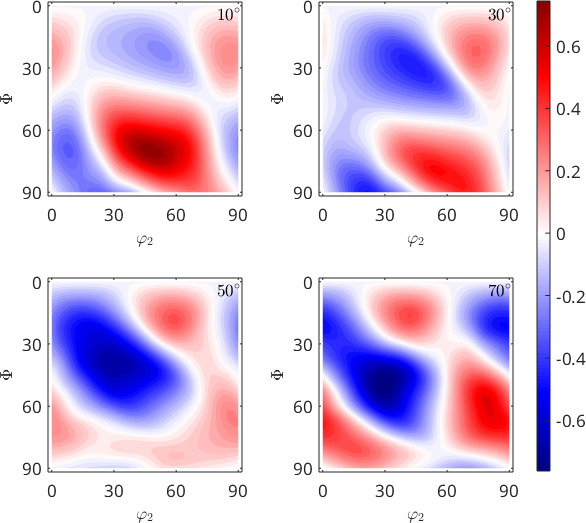

The Flux of a Vector Field

If we interpret the vector field W as a velocity field for the different crystal orientations. Then its divergence is a scalar field that indicates where orientations condense. In this interpretation a sink corresponds to negative flux / divergence and a source to positive flux / divergence.

flux = W.div

plot(flux,sP,'resolution',0.5*degree,'layout',[2 2],'faceAlpha',0.5)
mtexColorMap blue2red
mtexColorbar

hold on
plot(W,sP,'resolution',7.5*degree,'color','black')
hold off

flux = SO3FunHarmonic (432 → xyz)
  bandwidth: 32
  weight: 0

The Curl of a Vector Field

The counterpart of the flux is the curl of a vector field which describes the axis of local rotation within the crystal orientations

c = W.curl

plot(c,sP,'resolution',7.5*degree,'layout',[2 2],'color','black')

c = SO3VectorFieldHarmonic (432 → xyz)
  bandwidth: 32
  tangent space: leftVector

The Gradient of Orientation distribution Functions

A second natural usage of vector fields is as gradients of orientation dependent functions, e.g. ODF. Lets consider the following ODF of a quartz specimen

odf = SO3Fun.dubna

odf = SO3FunRBF (Quartz → xyz)
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 5°
  center: 19848 orientations, resolution: 5°
  weight: 1

Then its gradient is computed by the command odf.grad

g = odf.grad

g = SO3VectorFieldHarmonic (Quartz → xyz)
  bandwidth: 48
  tangent space: leftVector

Lets visualize the ODF together with its gradient in a sigma section plot

plot(odf,'sigma')
hold on
plot(g,'linewidth',1.5,'color','black','resolution',7.5*degree)
hold off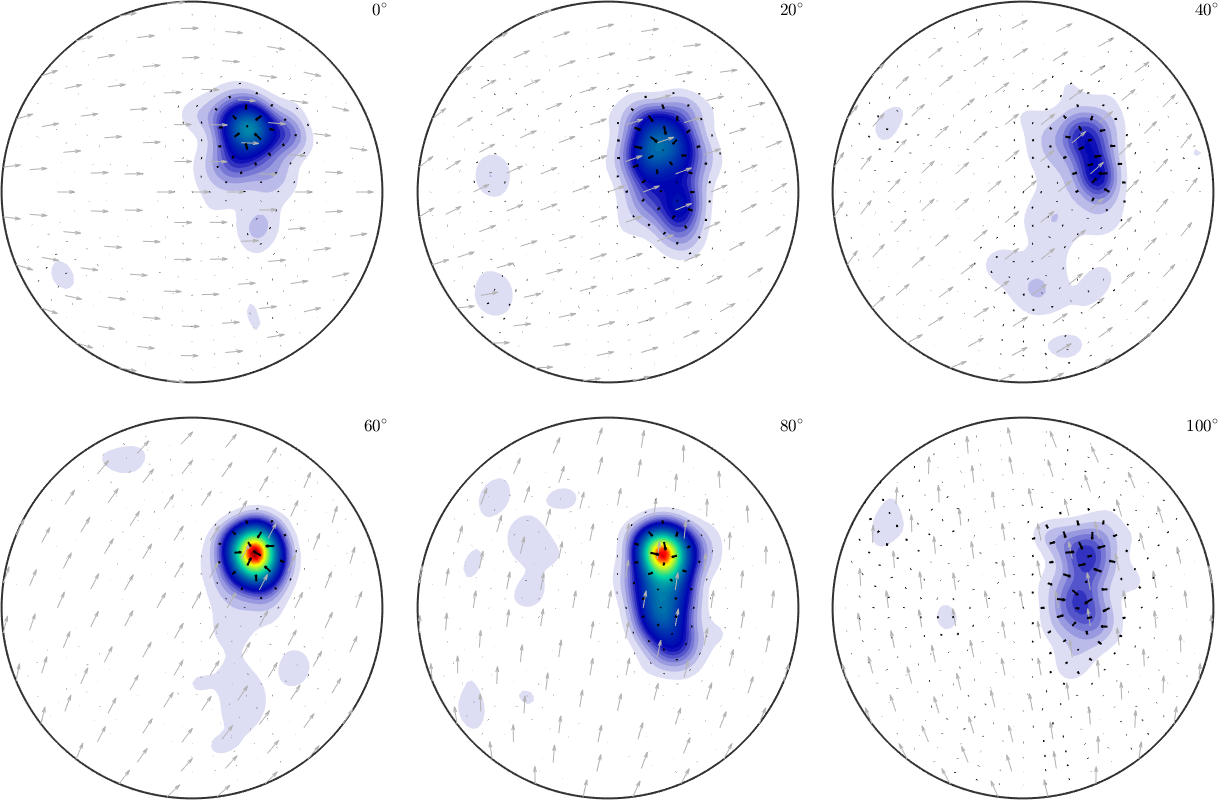

We observe how the gradients all points towards the closest local maximum. This is actually the foundation of the steepest descent algorithm used by MTEX in the commands max(odf) and calcComponents(odf)

As the gradient of a function is a vector field we may compute its curl and divergence. From mathematics we know that the curl must be zero

plot(g.curl,'sigma')

and the divergence coincides with the Laplacian of the

plot(g.div,'sigma',60*degree)
nextAxis
plot(laplace(SO3FunHarmonic(odf)),'sigma',60*degree)
mtexColorbar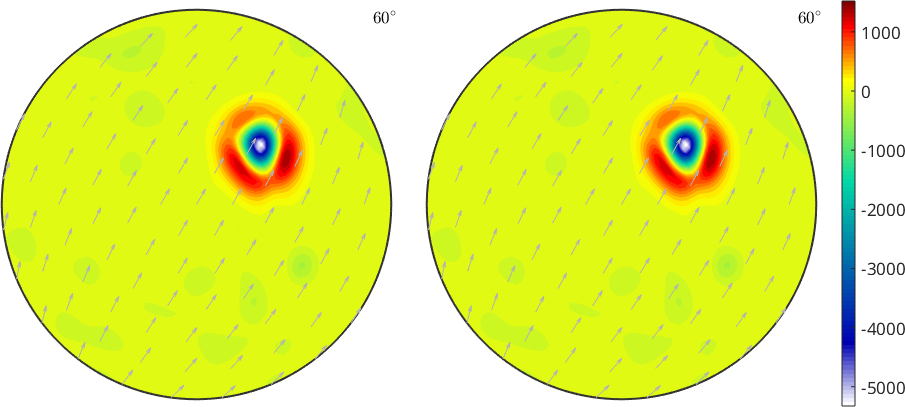

The fact that the curl of a vector field is zero is actually equivalent to the fact that the vector field is the gradient of some potential field, which can be computed by the command antiderivative(g) and coincides exactly with the original ODF odf.

odf2 = g.antiderivative

plot(odf2,'sigma')

odf2 = SO3FunHarmonic (Quartz → xyz)
  bandwidth: 48
  weight: 0

Overview of Operations for Orientational Vector Fields

The following operations are defined for vector fields VF, VF1, VF2

basic arithmetic operations: sum, difference, scaling, quotient
inner product dot(VF1,VF2)
cross product dot(VF1,VF2)
norm norm(VF)
rotate rotate(VF,rot)
average mean(VF)

Definition of Orientational Vector Fields

Explicitly by an Anonymous Function

Analogous to SO3FunHandle we are able to define SO3VectorFields by an anonymous function.

% cubic symmetry
cs = crystalSymmetry('432')

% product of rotational axis and rotational angle
f = @(mori) axis(mori) .* angle(mori);

% define the vector field
VF = SO3VectorFieldHandle(f,cs,cs)

% evaluating the vector field gives what we expect
round(VF.eval(orientation.byAxisAngle(vector3d(1,2,3),10*degree)))

cs = crystalSymmetry
 
  symmetry: 432    
  elements: 24     
  a, b, c : 1, 1, 1
 
 
VF = SO3VectorFieldHandle (432 → 432)
  tangent space: leftVector
 
 
ans = SO3TangentVector
 TagentSpace: leftVector
  x y z
  1 2 3

But plotting does not -- TODO!!!

% plot it
quiver3(VF,'axisAngle','resolution',7.5*degree,'color','black','linewidth',2)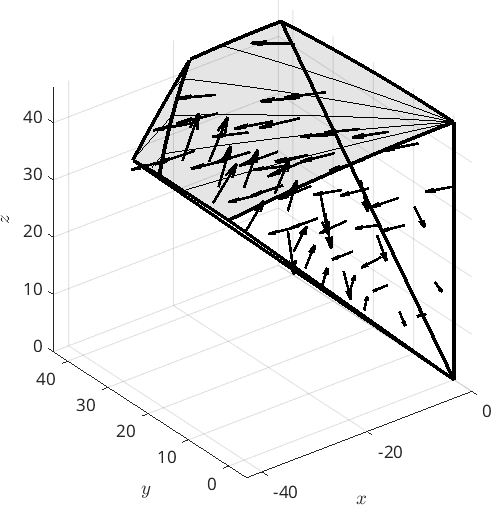

Definition via SO3VectorField

We can expand any SO3VectorField in an SO3VectorFieldHarmonic directly by the command SO3VectorFieldHarmonic

SO3VectorFieldHarmonic(VF)

ans = SO3VectorFieldHarmonic (432 → 432)
  bandwidth: 64
  tangent space: leftVector

Definition via function values

At first we need some example rotations

nodes = equispacedSO3Grid(specimenSymmetry('1'),'points',1e3);
nodes = nodes(:);

Next, we define function values for the rotations

y = vector3d.byPolar(sin(3*nodes.angle), nodes.phi2+pi/2);

Now the actual command to get SO3VF1 of type SO3VectorFieldHarmonic

SO3VF1 = SO3VectorFieldHarmonic.approximation(nodes, y,'bandwidth',16)

Warning: The given vector3d values v are assumed to describe elements
w.r.t. the left side tangent space. If you want them to be right
sided use SO3TangentVector(v,SO3TangentSpace.rightVector) instead. 
Warning: The oversampling factor in the approximation process is
0.3071. This could lead to a bad approximation. You may should use
the option 'regularization' in the option list of the approximation
method. 
 
SO3VF1 = SO3VectorFieldHarmonic (xyz → xyz)
  bandwidth: 16
  tangent space: leftVector

Definition via function handle

If we have a function handle for the function we could create a S2VectorFieldHarmonic via quadrature. At first lets define a function handle which takes rotation as an argument and returns a vector3d:

Now we can call the quadrature command to get SO3VF2 of type SO3VectorFieldHarmonic

SO3VF2 = SO3VectorFieldHarmonic.quadrature(@(v) f(v))

SO3VF2 = SO3VectorFieldHarmonic (xyz → xyz)
  bandwidth: 64
  tangent space: leftVector

Definition via SO3FunHarmonic

If we directly call the constructor with a multivariate SO3FunHarmonic with three entries it will create a SO3VectorFieldHarmonic with SO3F(1), SO3F(2), and SO3F(3) the \(x\), \(y\), and \(z\) component.

SO3F = SO3FunHarmonic(rand(1e3, 3))
SO3VF3 = SO3VectorFieldHarmonic(SO3F)

SO3F = SO3FunHarmonic (xyz → xyz)
  isReal: false
  size: 3 x 1
  bandwidth: 9
  weight: 0.77
 
 
SO3VF3 = SO3VectorFieldHarmonic (xyz → xyz)
  isReal: false
  bandwidth: 9
  tangent space: leftVector