Orientation maps determined by EBSD or any other technique are, as all experimental data, effected by measurement errors. Those measurement errors can be divided into systematic errors and random errors. Systematic errors mostly occur due to a bad calibration of the EBSD system and require additional knowledge to be corrected. Deviations from the true orientation due to noisy Kikuchi pattern or tolerances of the indexing algorithm can be modeled as random errors. In this section we demonstrate how random errors can be significantly reduced using denoising techniques.
We shall demonstrate the denoising capabilities of MTEX at the hand of an orientation map of deformed Magnesium
% import the data
mtexdata ferrite
% consider only indexed data
ebsd = ebsd('indexed');
% reconstruct the grain structure
[grains,ebsd.grainId] = calcGrains(ebsd,'angle',10*degree,'minPixel',5);
% smooth grain boundaries
grains = smooth(grains,5);
% plot the orientation map
plot(ebsd,ebsd.orientations)
% and on top the grain boundaries
hold on
plot(grains.boundary,'linewidth',1.5)
hold offebsd = EBSD (y↑→x)
Phase Orientations Mineral Color Symmetry Crystal reference frame
-1 1 (0.0016%) notIndexed
0 63044 (100%) Ferrite LightSkyBlue 432
Properties: ci, fit, iq, sem_signal
Scan unit : um
X x Y x Z : [0, 70] x [0, 70] x [0, 0]
Normal vector: (0,0,1)
A Very Sparse Measured Data Set
Although the data set has already some not indexed pixels we artificially make the situation more worse by throwing away 75 percent of all data.
ebsdSub = ebsd(discretesample(length(ebsd),round(length(ebsd)*25/100)));
% plot the reduced data
plot(ebsdSub,ebsdSub.orientations)
Our aim is now to recover the original orientation map. In a first step we reconstruct the grain structure from the remaining 25 percent of pixels.
% reconstruct the grain structure
[grainsSub,ebsdSub.grainId] = calcGrains(ebsdSub('indexed'),'angle',10*degree,'minPixel',2);
grainsSub = smooth(grainsSub,5);
hold on
plot(grainsSub.boundary,'linewidth',1.5)
hold off
The easiest way to reconstruct missing data is to use the command fill which interpolates missing data using the method of nearest neighbor. It is recommended to pass the grain structure grainsSub as an additional argument to the fill function. In this case the nearest neighbors are chosen within the grains.
ebsdSub_filled = fill(ebsdSub('indexed'),grainsSub);
plot(ebsdSub_filled('indexed'),ebsdSub_filled('indexed').orientations);
hold on
plot(grainsSub.boundary,'linewidth',1.5)
hold off
A much more powerful method is to use any denoising method and set the option 'fill'.
F = halfQuadraticFilter;
F.alpha = 0.25;
% interpolate the missing data
ebsdSub_filled = smooth(ebsdSub('indexed'),F,'fill',grainsSub);
plot(ebsdSub_filled('indexed'),ebsdSub_filled('indexed').orientations);
hold on
plot(grainsSub.boundary,'linewidth',1.5)
hold off
An Example from Geoscience
Data sets with many missing pixels most often appear when measuring geological samples. The following data set of forsterite contains about 25 percent missing pixels. Lets start by importing the data and reconstructing the grain structure.
close all;
mtexdata forsterite silent
ebsd = ebsd(inpolygon(ebsd,[10 4 5 3]*10^3));
plot(ebsd('Fo'),ebsd('Fo').orientations)
hold on
plot(ebsd('En'),ebsd('En').orientations)
plot(ebsd('Di'),ebsd('Di').orientations)
% compute and smooth grains
[grains,ebsd.grainId] = calcGrains(ebsd('indexed'),'angle',10*degree,'minPixel',3);
grains = smooth(grains,5);
% plot the boundary of all grains
plot(grains.boundary,'linewidth',2)
hold off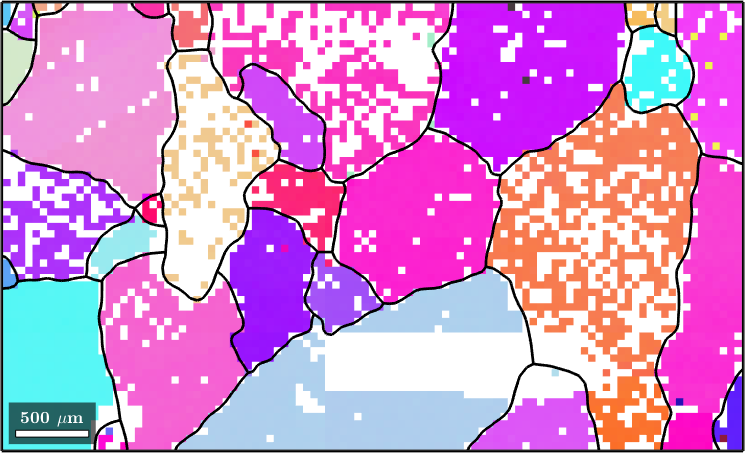
Using the option 'fill' the command smooth fills the holes inside the grains. Note that the nonindexed pixels at the grain boundaries are kept untouched. In order to allow MTEX to decide whether a pixel is inside a grain or not, the grains variable has to be passed as an additional argument.
F = halfQuadraticFilter;
F.alpha = 10;
ebsdS = smooth(ebsd('indexed'),F,'fill',grains);
plot(ebsdS('Fo'),ebsdS('Fo').orientations)
hold on
plot(ebsdS('En'),ebsdS('En').orientations)
plot(ebsdS('Di'),ebsdS('Di').orientations)
% plot the boundary of all grains
plot(grains.boundary,'linewidth',1.5)
% stop override mode
hold off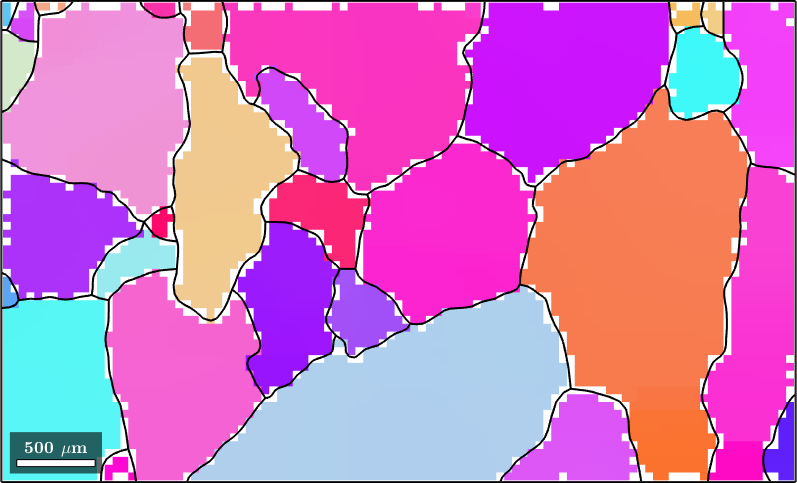
In order to visualize the orientation gradient within the grains, we plot the misorientation to the meanorientation. We observe that the mis2mean varies smoothly also within the regions of not indexed orientations.
% plot mis2mean for all phases
ipfKey = axisAngleColorKey(ebsdS('Fo'));
ipfKey.oriRef = grains(ebsdS('fo').grainId).meanOrientation;
ipfKey.maxAngle = 2.5*degree;
color = ipfKey.orientation2color(ebsdS('Fo').orientations);
plot(ebsdS('Fo'),color,'micronbar','off')
hold on
ipfKey.oriRef = grains(ebsdS('En').grainId).meanOrientation;
plot(ebsdS('En'),ipfKey.orientation2color(ebsdS('En').orientations))
% plot boundaries
plot(grains.boundary,'linewidth',4)
plot(grains('En').boundary,'lineWidth',4,'lineColor','r')
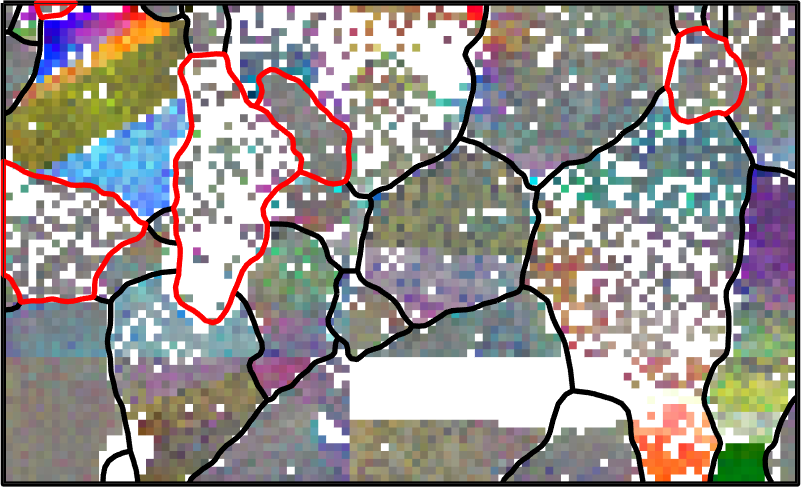
hold off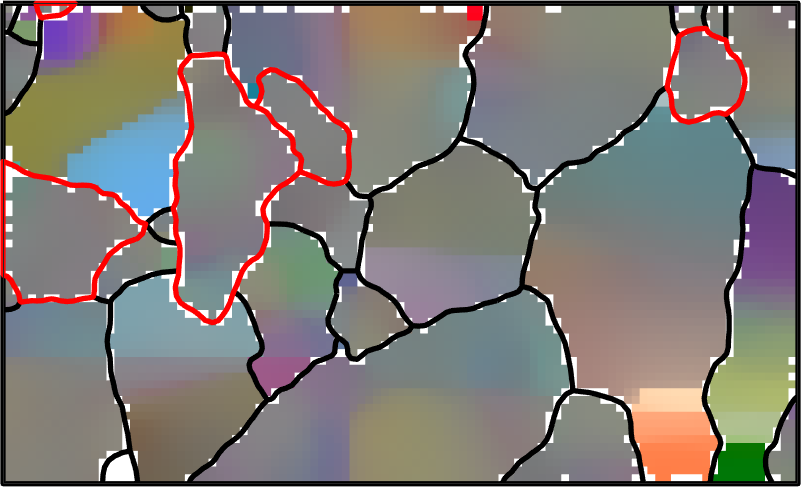
For comparison
ipfKey.oriRef = grains(ebsd('fo').grainId).meanOrientation;
ipfKey.maxAngle = 2.5*degree;
color = ipfKey.orientation2color(ebsd('Fo').orientations);
plot(ebsd('Fo'),color,'micronbar','off')
hold on
ipfKey.oriRef = grains(ebsd('En').grainId).meanOrientation;
plot(ebsd('En'),ipfKey.orientation2color(ebsd('En').orientations))
% plot boundaries
plot(grains.boundary,'linewidth',4)
plot(grains('En').boundary,'lineWidth',4,'lineColor','r')
hold off