Default is \(\vec c\) axis of highest symmetry.
TODO: Explain the default setting in more detail.
Switching between different Alignment Options
Since, especially for lower symmetry groups, different conventions for aligning the crystal axes are used it might be necessary to transform data, e.g, orientations or tensors, from one convention into another. This can be done using the command transformReferenceFrame as it illustrated below.
First we import the stiffness tensor Forsterite with respect to the axes alignment
cs = crystalSymmetry('mmm',[4.7646 10.2296 5.9942],'mineral','Olivin');
% import some stiffness tensor
fname = fullfile(mtexDataPath,'tensor','Olivine1997PC.GPa');
C = stiffnessTensor.load(fname,cs)
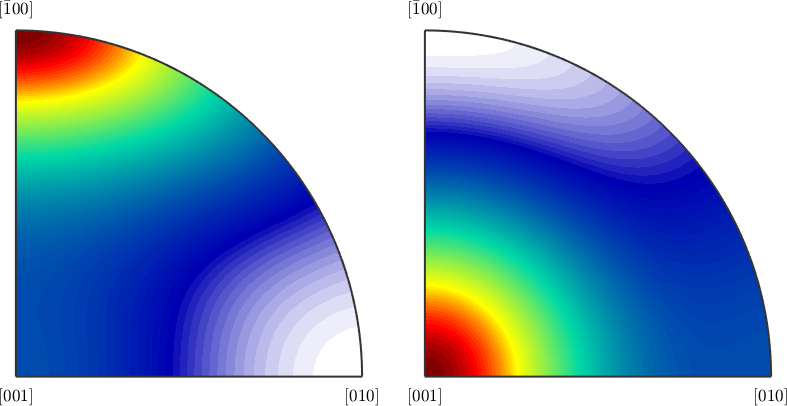
plot(C)C = stiffnessTensor (Olivin)
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
320.5 68.2 71.6 0 0 0
68.2 196.5 76.8 0 0 0
71.6 76.8 233.5 0 0 0
0 0 0 64 0 0
0 0 0 0 77 0
0 0 0 0 0 78.7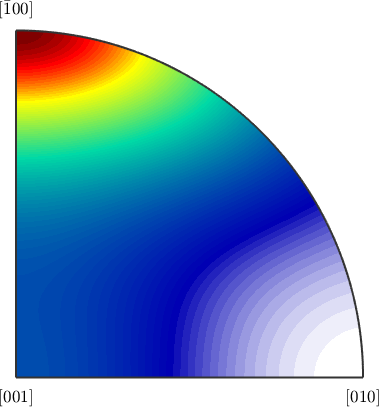
Let us now consider a different setup of the Forsterite symmetry, where the \(\vec a\) axis is the longest and the \(\vec c\)-axis is the shortest.
cs_new = crystalSymmetry('mmm',[10.2296 5.9942 4.7646],'mineral','Olivin')cs_new = crystalSymmetry
mineral : Olivin
symmetry: mmm
elements: 8
a, b, c : 10, 6, 4.8In order to represent the stiffness tensor C with respect to this setup we use the command transformReferenceFrame.
C_new = C.transformReferenceFrame(cs_new)
nextAxis
plot(C_new)C_new = stiffnessTensor (Olivin)
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
196.5 76.8 68.2 0 0 0
76.8 233.5 71.6 0 0 0
68.2 71.6 320.5 0 0 0
0 0 0 77 0 0
0 0 0 0 78.7 0
0 0 0 0 0 64