Variables of type grain3d store 3D grain data. At the moment 3d grains can be imported from <NeperInterface.html Neper% > or from Dream3d.
Import Grains from Dream3d
As with any data we can import
% specify the file name
fname = fullfile(mtexDataPath,'EBSD','SmallIN100_MeshStats.dream3d');
grains = grain3d.load(fname);
% for triangulated data sets it may be useful to plot them without lines
plot(grains,grains.meanOrientation,'LineStyle','none','micronbar','off')
% use a nice plotting convention
how2plot = plottingConvention.default3D;
setCamera(how2plot)
Similarly as with two dimensional grains we can select individual grains by arbitrary constraints. For instance we can find the largest grain by
% index of the grain with the largest volume
[~,id] = max(grains.volume)
plot(grains(id),'edgeAlpha',0.15,'micronBar','off')
setCamera(how2plot)id =
146
Lets finally plot a slice through this 3d data set
% define the plane by a normal direction and a point
plane = plane3d(vector3d(1,1,1),vector3d(-20,20,-15));
% compute the sliced grains
grains2 = slice(grains,plane)
% plot them
plot(grains2,grains2.meanOrientation)grains2 = grain2d (y↑→x)
Phase Grains Pixels Mineral Symmetry Crystal reference frame
2 187 187 unknown 622 X||a*, Y||b, Z||c*
boundary segments: 7177 (655 µm)
inner boundary segments: 0 (0 µm)
triple points: 269
Properties: meanRotation, Id3d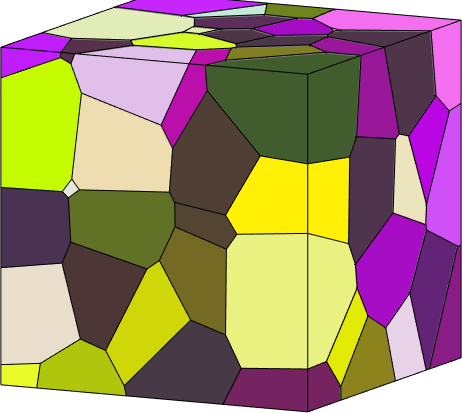
Import Grains from Neper
Neper is a software package for the simulation of three dimensional microstructures. After installation it can be directly called by MTEX. The general workflow is explained here. Here we use it to quickly generate a copper microstructure with specific texture and specific distribution of boundary normals.
% set up the communication with Neper
job = neperInstance;
% define a texture
cs = crystalSymmetry.load('quartz.cif','color','lightblue');
odf = fibreODF(cs.cAxis,vector3d(1,1,1));
numGrains=100;
grains = job.simulateGrains(odf,numGrains,'silent')
% or you can load an existing tessellation file
%grains = grain3d.load('allgrains.tess','CS',cs)grains = grain3d
Phase Grains Volume Mineral Symmetry Crystal reference frame
2 100 1 Quartz 321 X||a*, Y||b, Z||c*
boundary faces: 629
Properties: meanRotation% colorize by mean orientation
plot(grains,grains.meanOrientation,'micronbar','off','faceAlpha',0.5)
setCamera(how2plot)
Slicing
To get the usually used 2d grain data, it is possible to slice 3d grains by different methods.
% make all slices passing through the center point of the cube
P0 = vector3d(0.5,0.5,0.5);
% with normal (1,-1,1)
N = vector3d(1,-1,1);
grains_2d = grains.slice(N,P0)
plot(grains_2d,grains_2d.meanOrientation,'micronbar','off','linewidth',2)
setCamera(how2plot)grains_2d = grain2d (y↑→x)
Phase Grains Pixels Mineral Symmetry Crystal reference frame
2 40 40 Quartz 321 X||a*, Y||b, Z||c*
boundary segments: 123 (16 µm)
inner boundary segments: 0 (0 µm)
triple points: 62
Properties: meanRotation, Id3d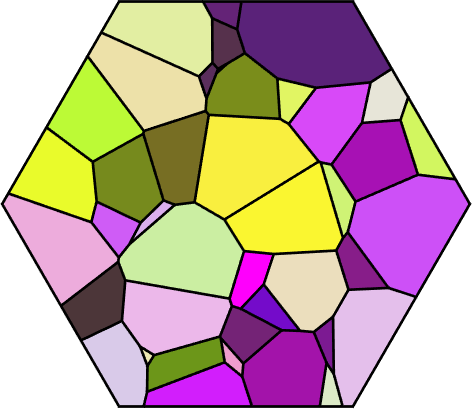
It might be reasonable to adjust the plotting convention such that the normal direction N points out of screen.
how2plot = plottingConvention;
how2plot.outOfScreen = N; how2plot.east = vector3d(1,1,0);
setCamera(how2plot), axis off, xlabel('') , ylabel('')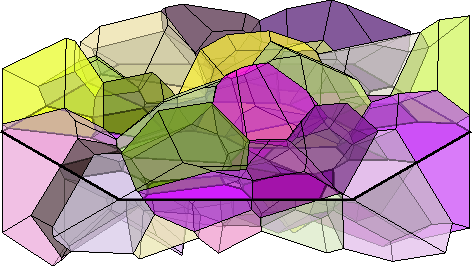
Grains intersecting a slice
Using the function intersected we can identify all grains that intersect a given plane. Lets simply add 3d the shapes of all grains intersecting the plane.
isInter = grains.intersected(N,P0);
[a,b,c] = grains(isInter).principalComponents;
hold on
plot(grains(isInter),grains(isInter).meanOrientation,'faceAlpha',0.5)
%plotEllipsoid(grains(isInter).centroid,a,b,c,'faceAlpha',0.5)
hold off
how2plot.north = N;
how2plot.outOfScreen = vector3d(1,-1,-1);
setCamera(how2plot)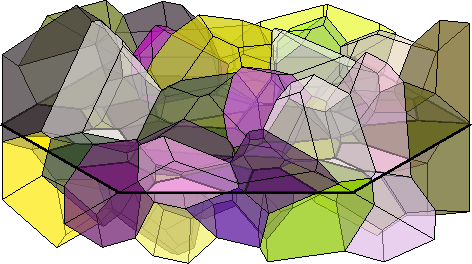
Plot the normal directions of one grain
%grains = grains(1)
%dir = grains.I_GF(1,:)' .* grains.boundary.N % flip according to I_GF
%quiver(grains.boundary,dir)
%plot(grains)