Functions on the circle are periodic functions. Hence they may be represented as weighted sums of sines and cosines (Fourier series). A spherical function \(f\) can be written as series of the form
\[ f(x) = \sum_{k=-N}^N \hat f_k e^{-ikx} \]
with respect to Fourier coefficients \(\hat f_k\). Note that \(f\) is \(2\pi\)-periodic.
Within the class S1FunHarmonic spherical functions are represented by their Fourier coefficients which are stored in the field fun.fhat. As an example lets define a Fourier series which Fourier coefficients \(\hat f_0 = 1\), \(\hat f_1 = 0\), \(\hat f_{-1} = 3\), \(\hat f_2 = 4\) and \(\hat f_{-2} = 0\)
fun = S1FunHarmonic([0;3;1;0;4])
clf
plot(fun)fun = S1FunHarmonic
bandwidth: 2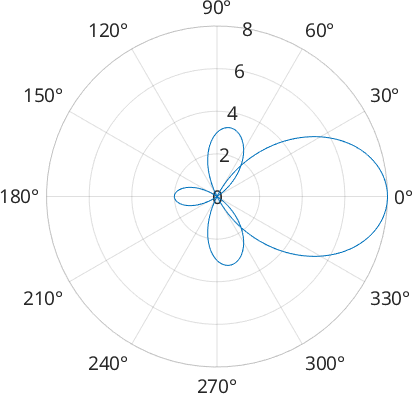
ans =
Line with properties:
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 0.5000
Marker: 'none'
MarkerSize: 10.5000
MarkerFaceColor: 'none'
ThetaData: [0 0.0175 0.0349 0.0524 0.0698 0.0873 … ] (1×361 double)
RData: [8 7.9971 7.9884 7.9740 7.9538 7.9278 … ] (1×361 double)
Use GET to show all properties
More practically, periodic functions appear after density estimation from circular data, e.g. of the azimuth angle of three dimensional vectors
% some random directions
v = vector3d.rand(1000);
% perform density estimation of the azimuth angle
fun = calcDensity(v.rho,'periodic')
clf
plot(fun,'linewidth',2)fun = S1FunHarmonic
bandwidth: 61
isReal: true
ans =
Line with properties:
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 2
Marker: 'none'
MarkerSize: 10.5000
MarkerFaceColor: 'none'
ThetaData: [0 0.0175 0.0349 0.0524 0.0698 0.0873 … ] (1×361 double)
RData: [1.0290 1.0853 1.1403 1.1874 1.2226 … ] (1×361 double)
Use GET to show all properties