by Dr. Marco Witte, Salzgitter Mannesmann Forschung, March 2020.
The magnetocrystalline anisotropy energy Ea is necessary to rotate all magnetic moments towards the direction of an external field (saturation). This texture dependent property is of special interest for electrical steels.
This example script is based on the following literature: * Wu et al. (2017): Journal of Magnetism and Magnetic Materials 444: 211–217. * Bunge, H.-J. (2013): Texture analysis in materials science: mathematical methods. * Bunge, H. J. (1989): Texture and magnetic properties. Textures and microstructures, 11. * Szpunar, J. (1989): Texture, Stress, and Microstructure 11, 2-4: 93-105. * Landgraf et al.(2003): Journal of Magnetism and Magnetic Materials 254–255: 364–66.
Define Parameters
% alloy content of Si and Al in wt.%
x_Si = 3;
x_Al = 1;
% magnetic anisotropy constant
K1 = 4.77 - 0.21256*x_Si - 0.03816*x_Al;
% magnetic saturation J_S depends on alloy composition
J_S = 2.162 - 0.043*x_Si - 0.0625*x_Al;
% crystal symmetry
CS = crystalSymmetry('m-3m');
% define an odf - here with Goss orientation, as desired for grain oriented
% electrical steel
odf = unimodalODF(orientation.goss(CS));
% simulate random orientations from the ODF
ori = discreteSample(odf,10000);Calculate anisotropy energy for different external magnetic field directions in sheet plane
Due to the rotation of an electrical motor the field direction is changing constantly inside the sheet plane.
% rotation from 0 - 90 degree
rot_mag = 0:10:90;
% initialize variable for storage
E_a = zeros(length(rot_mag),length(ori));
% loop over all rotations
for j = 1:length(rot_mag)
% rotate orientations
rot = rotation.byAxisAngle(zvector,rot_mag(j)*degree);
ori_rot = rot * ori;
% determine uvw of orientations (makes loop necessary)
ori_uvw = inv(ori_rot) * xvector;
% direction cosines with direction <100> of easy magnetization
cos_val_1 = cos(angle(Miller(1,0,0,CS),ori_uvw,'noSymmetry'));
cos_val_2 = cos(angle(Miller(0,1,0,CS),ori_uvw,'noSymmetry'));
cos_val_3 = cos(angle(Miller(0,0,1,CS),ori_uvw,'noSymmetry'));
% calculate magnetic anisotropy energy
E_a(j,:) = K1*(cos_val_1.^2.*cos_val_2.^2 + ...
cos_val_2.^2.*cos_val_3.^2 + cos_val_1.^2.*cos_val_3.^2);
endcalculate magnetization J_50 at H = 5000 A/m (J_50 is supposed to depend only on texture
J_50 = J_S*(1-0.19*mean(E_a,2));
%plot results
figure
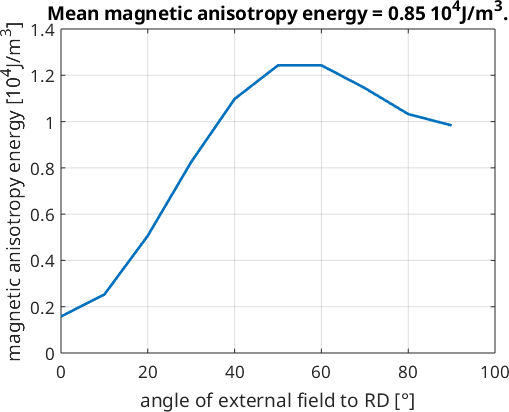
plot(rot_mag,mean(E_a,2),'LineWidth',2)
ylabel('magnetic anisotropy energy [10^4J/m^3]')
xlabel('angle of external field to RD [°]')
grid on
title(['Mean magnetic anisotropy energy = ' num2str(mean(mean(E_a)),'%.2f') ' 10^4J/m^3.'],'fontsize',14)
figure
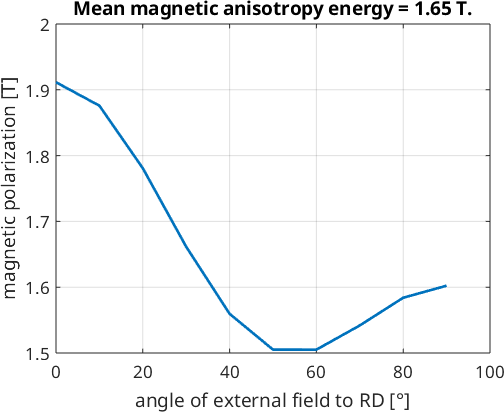
plot(rot_mag,mean(J_50,2),'LineWidth',2)
ylabel('magnetic polarization [T]')
xlabel('angle of external field to RD [°]')
grid on
title(['Mean magnetic anisotropy energy = ' num2str(mean(mean(J_50)),'%.2f') ' T.'],'fontsize',14)