CSL Boundaries

CSL Boundaries edit page

In this section we consider the analysis of CSL boundaries. Therefore lets start by importing some Iron data and reconstructing the grain structure.

mtexdata csl
plotx2east

% grain segmentation
[grains,ebsd.grainId] = calcGrains(ebsd('indexed'));

% grain smoothing
grains = smooth(grains,5);

% plot the result
plot(grains,grains.meanOrientation)

ebsd = EBSD
 
 Phase   Orientations  Mineral         Color  Symmetry  Crystal reference frame
    -1  154107 (100%)     iron  LightSkyBlue      m-3m                         
 
 Properties: ci, error, iq
 Scan unit : um
 X x Y x Z : [0 511] x [0 300] x [0 0]
 Normal vector: (0,0,1)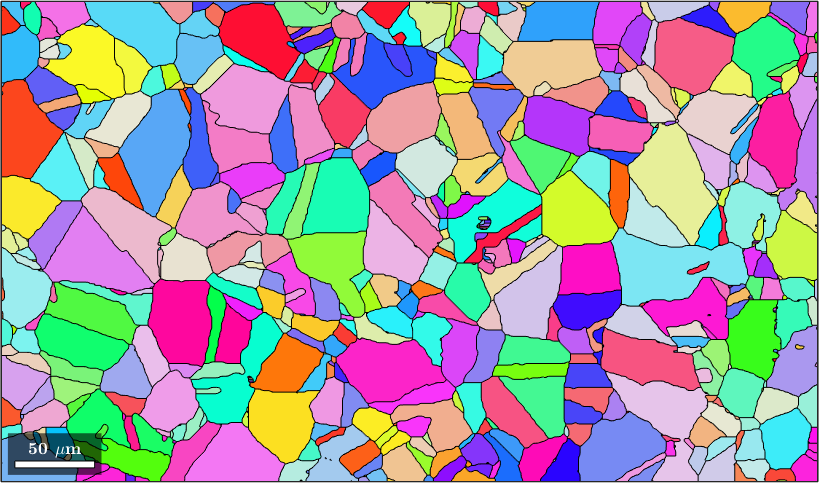

Next we plot image quality as it makes the grain boundaries visible. and overlay it with the orientation map

plot(ebsd,log(ebsd.prop.iq),'figSize','large')
mtexColorMap black2white
setColorRange([.5,5])

% the option 'FaceAlpha',0.4 makes the plot a bit translucent
hold on
plot(grains,grains.meanOrientation,'FaceAlpha',0.4,'linewidth',3)
hold off

Detecting CSL Boundaries

In order to detect CSL boundaries within the data set we first restrict the grain boundaries to iron to iron phase transitions and check then the boundary misorientations to be a CSL(3) misorientation with threshold of 3 degree.

% restrict to iron to iron phase transition
gB = grains.boundary('iron','iron')

% select CSL(3) grain boundaries
gB3 = gB(angle(gB.misorientation,CSL(3,ebsd.CS)) < 3*degree);

% overlay CSL(3) grain boundaries with the existing plot
hold on
plot(gB3,'lineColor','gold','linewidth',3,'DisplayName','CSL 3')
hold off

gB = grainBoundary
 
 Segments    length  mineral 1  mineral 2
    20356  16362 µm       iron       iron

Mark triple points

Next we want to mark all triple points with at least 2 CSL boundaries

% logical list of CSL boundaries
isCSL3 = grains.boundary.isTwinning(CSL(3,ebsd.CS),3*degree);

% logical list of triple points with at least 2 CSL boundaries
tPid = sum(isCSL3(grains.triplePoints.boundaryId),2)>=2;

% plot these triple points
hold on
plot(grains.triplePoints(tPid),'color','red','linewidth',2,'MarkerSize',8)
hold off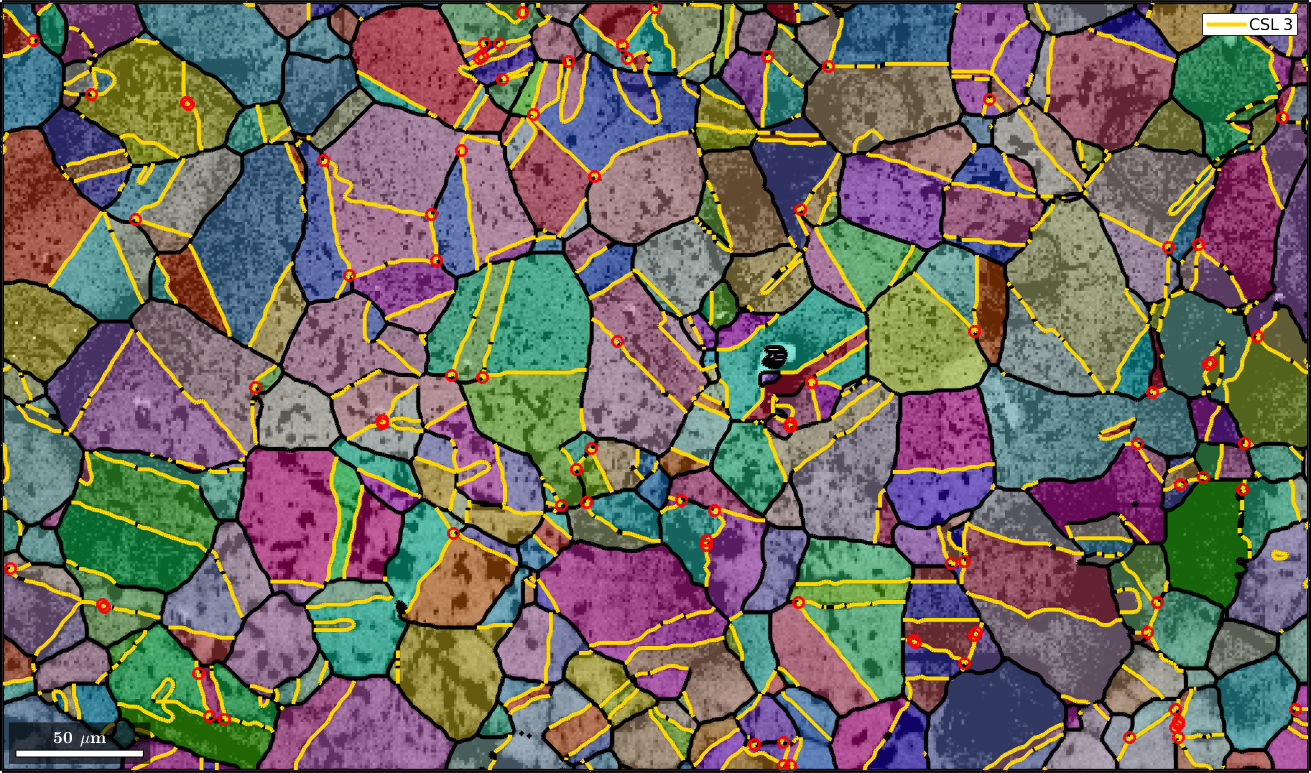

Merging grains with common CSL(3) boundary

Next we merge all grains together which have a common CSL(3) boundary. This is done with the command merge.

% this merges the grains
[mergedGrains,parentIds] = merge(grains,gB3);

% overlay the boundaries of the merged grains with the previous plot
hold on
plot(mergedGrains.boundary,'linecolor','w','linewidth',3)
hold off

Finaly, we check for all other types of CSL boundaries and overlay them with our plot.

delta = 5*degree;
gB5 = gB(gB.isTwinning(CSL(5,ebsd.CS),delta));
gB7 = gB(gB.isTwinning(CSL(7,ebsd.CS),delta));
gB9 = gB(gB.isTwinning(CSL(9,ebsd.CS),delta));
gB11 = gB(gB.isTwinning(CSL(11,ebsd.CS),delta));

hold on
plot(gB5,'lineColor','b','linewidth',2,'DisplayName','CSL 5')
hold on
plot(gB7,'lineColor','g','linewidth',2,'DisplayName','CSL 7')
hold on
plot(gB9,'lineColor','m','linewidth',2,'DisplayName','CSL 9')
hold on
plot(gB11,'lineColor','c','linewidth',2,'DisplayName','CSL 11')
hold off

Misorientations in the 3d fundamental zone

We can also look at the boundary misorientations in the 3 dimensional fundamental orientation zone.

% compute the boundary of the fundamental zone
oR = fundamentalRegion(ebsd.CS,ebsd.CS,'antipodal');
close all
plot(oR)

% plot 500 random misorientations in the 3d fundamental zone
mori = discreteSample(gB.misorientation,500);
hold on
plot(mori.project2FundamentalRegion)
hold off

% mark the CSL(3) misorientation
hold on
csl3 = CSL(3,ebsd.CS);
plot(csl3.project2FundamentalRegion('antipodal') ,'MarkerColor','r','DisplayName','CSL 3','MarkerSize',20)
hold off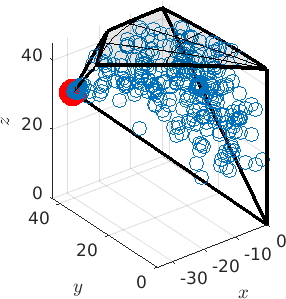

Analyzing the misorientation distribution function

In order to analyze more quantitatively the boundary misorientation distribution we can compute the so called misorientation distribution function. The option antipodal is applied since we want to identify mori and inv(mori).

mdf = calcDensity(gB.misorientation,'halfwidth',5*degree,'bandwidth',48)

mdf = SO3FunHarmonic (iron → iron)
  antipodal: true
  bandwidth: 48
  weight: 1

Next we can visualize the misorientation distribution function in axis angle sections.

plot(mdf,'axisAngle',(25:5:60)*degree,'colorRange',[0 15])

annotate(CSL(3,ebsd.CS),'label','\(CSL_3\)','backgroundcolor','w')
annotate(CSL(5,ebsd.CS),'label','\(CSL_5\)','backgroundcolor','w')
annotate(CSL(7,ebsd.CS),'label','\(CSL_7\)','backgroundcolor','w')
annotate(CSL(9,ebsd.CS),'label','\(CSL_9\)','backgroundcolor','w')

drawNow(gcm)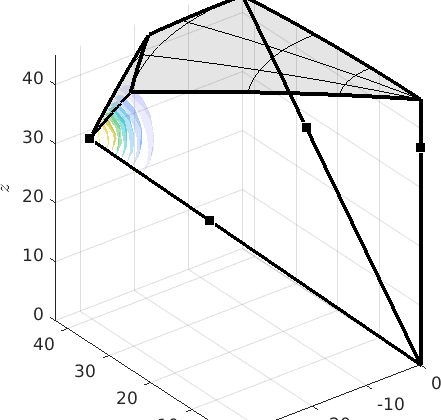

The MDF can be now used to compute preferred misorientations

[~,mori] = max(mdf,'numLocal',2)

mori = misorientation (iron → iron)
  size: 2 x 1
  antipodal:         true
 
  Bunge Euler angles in degree
     phi1     Phi    phi2
  115.714    47.5 209.286
  99.2934 27.4704 286.643

and their volumes in percent

100 * volume(gB.misorientation,CSL(3,ebsd.CS),2*degree)

100 * volume(gB.misorientation,CSL(9,ebsd.CS),2*degree)

ans =
   40.9904
ans =
    2.0338

or to plot the MDF along certain fibers

omega = linspace(0,60*degree);
fibre100 = orientation.byAxisAngle(xvector,omega,mdf.CS,mdf.SS)
fibre111 = orientation.byAxisAngle(vector3d(1,1,1),omega,mdf.CS,mdf.SS)
fibre101 = orientation.byAxisAngle(vector3d(1,0,1),omega,mdf.CS,mdf.SS)

close all
plot(omega ./ degree,mdf.eval(fibre100),'LineWidth',2)
hold on
plot(omega ./ degree,mdf.eval(fibre111),'LineWidth',2)
plot(omega ./ degree,mdf.eval(fibre101),'LineWidth',2)
hold off
legend('100','111','101')
xlabel('misorientation angle');
ylabel('mrd');

fibre100 = misorientation (iron → iron)
  size: 1 x 100
 
fibre111 = misorientation (iron → iron)
  size: 1 x 100
 
fibre101 = misorientation (iron → iron)
  size: 1 x 100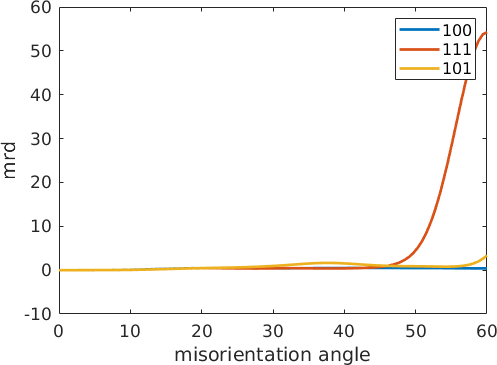

or to evaluate it in an misorientation directly

mori = orientation.byEuler(15*degree,28*degree,14*degree,mdf.CS,mdf.CS)

mdf.eval(mori)

mdf.eval(csl3)

mori = misorientation (iron → iron)
 
  Bunge Euler angles in degree
  phi1  Phi phi2
    15   28   14
 
ans =
    1.5276
ans =
   54.2486