Taylor Model edit page

Basic Settings

display pole figure plots with RD on top and ND west

plotx2north

% store old annotation style
storepfA = getMTEXpref('pfAnnotations');

% set new annotation style to display RD and ND
pfAnnotations = @(varargin) text(-[vector3d.X,vector3d.Y],{'RD','ND'},...
  'BackgroundColor','w','tag','axesLabels',varargin{:});

setMTEXpref('pfAnnotations',pfAnnotations);

Slip in Body Centered Cubic Materials

In the following we consider crystallographic slip in bcc materials

% define the slip systems in bcc
cs = crystalSymmetry('432');
sS = slipSystem.bcc(cs)
sS = slipSystem (432)
 size: 1 x 3
 
   u    v    w  | h    k    l CRSS
   1   -1    1    0    1    1    1
  -1    1    1    2    1    1    1
  -1    1    1    3    2    1    1

under plane strain

q = 0;
epsilon = strainTensor(diag([1 -q -(1-q)]))
epsilon = strainTensor (xyz)
  type: Lagrange 
  rank: 2 (3 x 3)
 
  1  0  0
  0  0  0
  0  0 -1

The orientation dependence of the Taylor factor

For a family of slip systems sS the Taylor factor M describes the total amount of slip activity that is required to deform a crystal in orientation ori according to strain epsilon. In MTEX this can be computed by the command calcTaylor.

% define a crystal orientation
ori = orientation.byEuler(0,30*degree,15*degree,cs)

% compute the Taylor factor
[M,b,W] = calcTaylor(inv(ori)*epsilon,sS.symmetrise);

M
W
ori = orientation (432 → xyz)
 
  Bunge Euler angles in degree
  phi1  Phi phi2
     0   30   15
 
M =
    2.1208
 
W = spinTensor (432)
  rank: 2 (3 x 3)
 
 *10^-2
      0     51  65.65
    -51      0 -23.04
 -65.65  23.04      0

When called without specifying an orientation the command calcTaylor computes the Taylor factor M as well as the spin tensors W as orientation dependent functions, which can be easily visualized and analyzed.

[M,~,W] = calcTaylor(epsilon,sS.symmetrise)

% evaluate the Taylor factor at an arbitrary orientation
M.eval(ori)
W.eval(ori)
M = SO3FunHarmonic (432 → xyz)
  bandwidth: 32
  weight: 3.1
 
 
W = SO3VectorFieldHarmonic (432 → xyz)
  bandwidth: 32
  tangent space: rightSpinTensor
 
ans =
    2.1009
 
ans = spinTensor (432)
  rank: 2 (3 x 3)
 
 *10^-2
      0  38.89  49.68
 -38.89      0 -14.97
 -49.68  14.97      0

The following code reproduces Fig. 5 of the paper of Bunge, H. J. (1970). Some applications of the Taylor theory of polycrystal plasticity. Kristall Und Technik, 5(1), 145-175. http://doi.org/10.1002/crat.19700050112 

% set up an phi1 section plot
sP = phi1Sections(cs);
sP.phi1 = (0:10:90)*degree;

% plot the Taylor factor
plot(M,'smooth',sP)
mtexColorbar

hold on
plot(W,'color','black')
hold off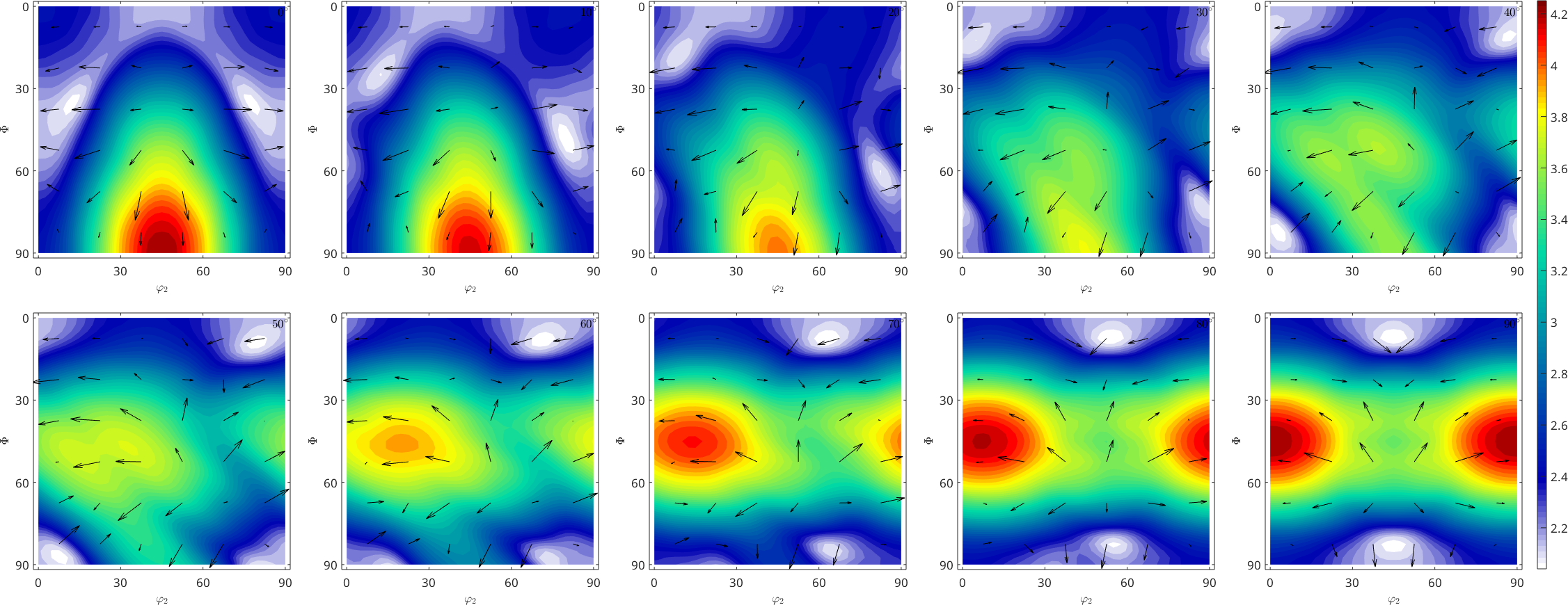

The orientation dependence of the spin

The norm of the spin tensor is exactly the angle of misorientation a crystal with the corresponding orientation experiences according to Taylor theory. Compare Fig. 8 of the above paper

plot(norm(W)/degree,'smooth',sP,'resolution',0.5*degree)
mtexColorbar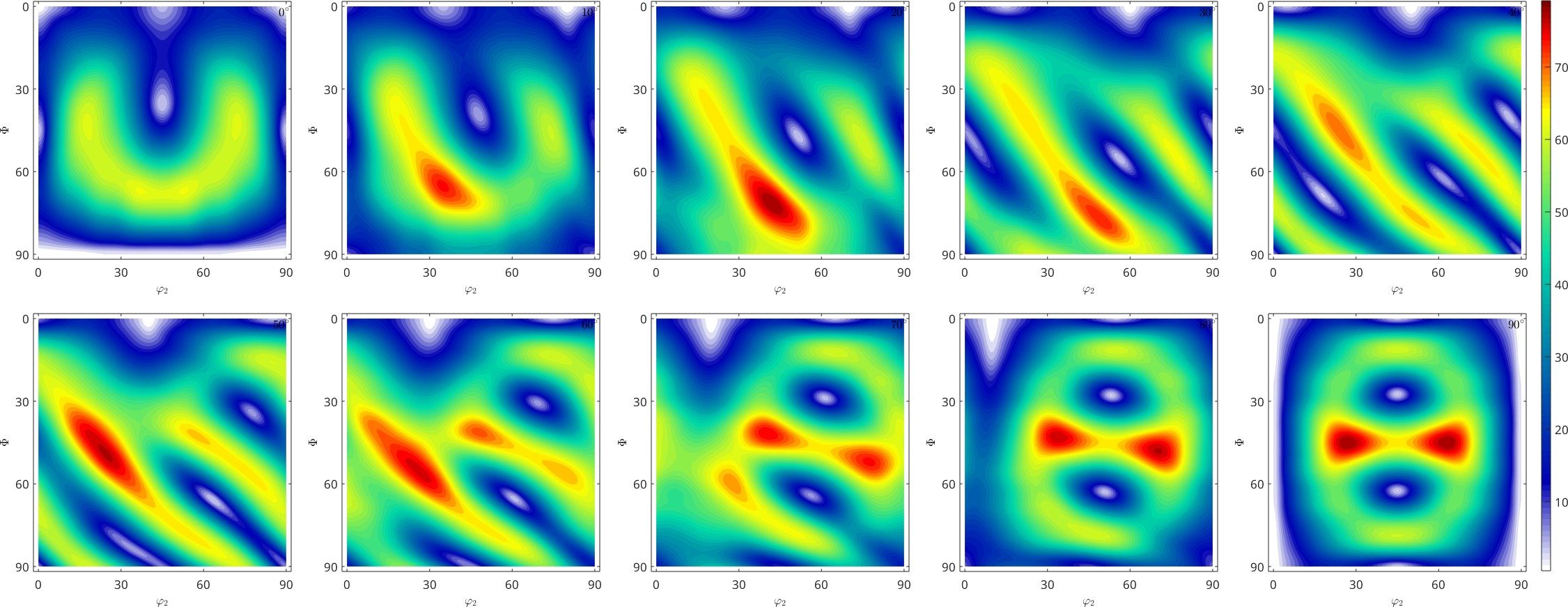

Display the crystallographic spin in sigma sections

sP = sigmaSections(cs,specimenSymmetry);
plot(norm(W)./degree,'smooth',sP)
mtexColorbar

Identification of the most active slip directions

Next we consider a real world data set

mtexdata csl

% compute grains
grains = calcGrains(ebsd('indexed'));
grains = smooth(grains,5);

% remove small grains
grains(grains.grainSize <= 2) = []
ebsd = EBSD
 
 Phase   Orientations  Mineral         Color  Symmetry  Crystal reference frame
    -1  154107 (100%)     iron  LightSkyBlue      m-3m                         
 
 Properties: ci, error, iq
 Scan unit : um
 X x Y x Z : [0 511] x [0 300] x [0 0]
 Normal vector: (0,0,1)
 
 
grains = grain2d
 
 Phase  Grains  Pixels  Mineral  Symmetry  Crystal reference frame
    -1     527  153693     iron      m-3m                         
 
 boundary segments: 23536 (17955 µm)
 inner boundary segments: 93 (71 µm)
 triple points: 1451
 
 Properties: meanRotation, GOS

and apply the Taylor model to each grain of our data set

% some strain
q = 0;
epsilon = strainTensor(diag([1 -q -(1-q)]))

% consider fcc slip systems
sS = symmetrise(slipSystem.fcc(grains.CS));

% apply Taylor model
[M,b,W] = calcTaylor(inv(grains.meanOrientation)*epsilon,sS);
epsilon = strainTensor (xyz)
  type: Lagrange 
  rank: 2 (3 x 3)
 
  1  0  0
  0  0  0
  0  0 -1
% colorize grains according to Taylor factor
plotzOutOfPlane, plotx2east
plot(grains,M)
mtexColorMap white2black
mtexColorbar

% index of the most active slip system - largest b
[~,bMaxId] = max(b,[],2);

% rotate the most active slip system in specimen coordinates
sSGrains = grains.meanOrientation .* sS(bMaxId);

% visualize slip direction and slip plane for each grain
hold on
quiver(grains,sSGrains.b,'autoScaleFactor',0.7,'displayName','Burgers vector','project2plane')
hold on
quiver(grains,sSGrains.trace,'autoScaleFactor',0.7,'displayName','slip plane trace')
hold off

plot the most active slip directions observe that they point all towards the lower hemisphere - why? they do change if q is changed

figure(2)
plot(sSGrains.b)
text([xvector,yvector,zvector],'labeled','BackGroundcolor','w')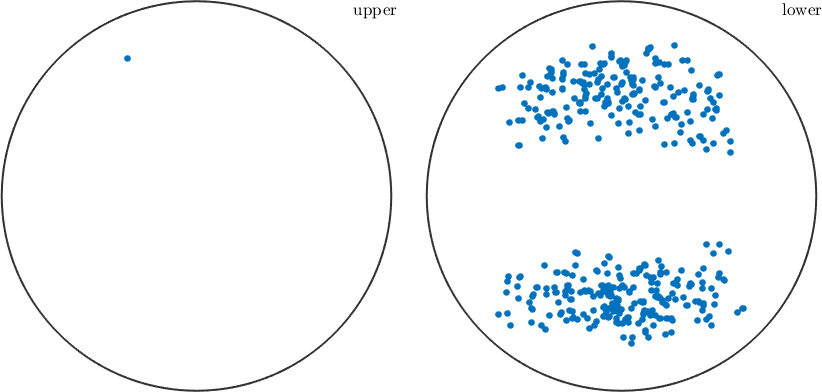

Texture evolution during rolling

% define some random orientations
rng(0)
ori = orientation.rand(1e5,grains.CS);

% 30 percent plane strain
q = 0;
epsilon = 0.3 * strainTensor(diag([1 -q -(1-q)]));

numIter = 100;

% compute the Taylor factors and the orientation gradients
[~,~,spin] = calcTaylor(epsilon ./ numIter, sS.symmetrise);

progress(0,numIter);
for sas=1:numIter

  % compute the Taylor factors and the orientation gradients
  W = spinTensor(spin.eval(ori).').';

  % rotate the individual orientations
  ori = ori .* orientation(-W);
  progress(sas,numIter);

end
% plot the resulting pole figures

% set new annotation style to display RD and ND
pfAnnotations = @(varargin) text([vector3d.X,vector3d.Y,vector3d.Z],{'RD','TD','ND'},...
  'BackgroundColor','w','tag','axesLabels',varargin{:});
setMTEXpref('pfAnnotations',pfAnnotations);

plotPDF(ori,Miller({0,0,1},{1,1,1},cs),'contourf')
mtexColorbar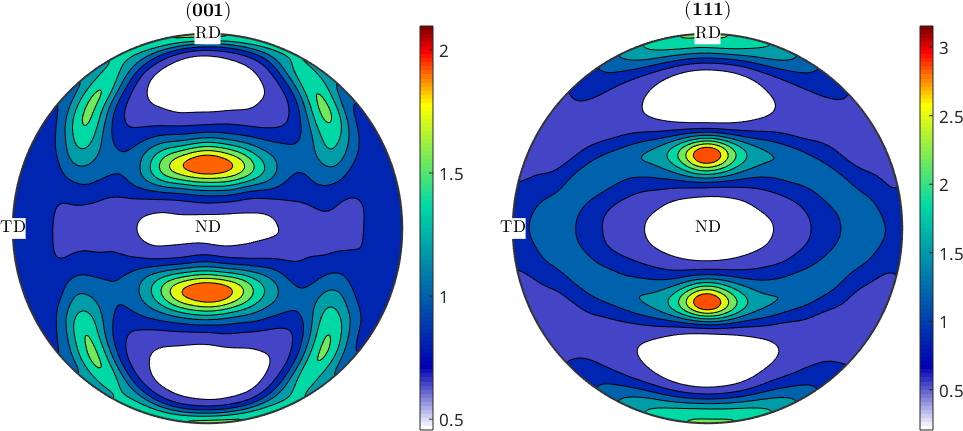

restore MTEX preferences

setMTEXpref('pfAnnotations',storepfA);