ODF Characteristics

ODF Characteristics edit page

Let us first begin with some constructed ODFs to be analyzed below

A bimodal ODF:

cs = crystalSymmetry('mmm');
odf1 = unimodalODF(orientation.byEuler(0,0,0,cs)) + ...
  unimodalODF(orientation.byEuler(30*degree,0,0,cs))

odf1 = SO3FunRBF (mmm → y↑→x)
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 10°
  center: 2 orientations
 
  Bunge Euler angles in degree
  phi1    Phi   phi2 weight
     0      0      0      1
    30      0      0      1

A fibre ODF:

f001_x = fibre(Miller(0,0,1,cs),xvector)

odf2 = fibreODF(f001_x)

f001_x = fibre (mmm → y↑→x)
 
  h || r: (001) || (1,0,0)
 
odf2 = SO3FunCBF (mmm → y↑→x)
 
  kernel: de la Vallee Poussin, halfwidth 10°
  fibre : (001) || 1,0,0
  weight: 1

An ODF estimated from diffraction data

mtexdata dubna

odf3 = calcODF(pf,'resolution',5*degree,'zero_Range')

pf = PoleFigure (y↑→x)
  crystal symmetry : Quartz (321, X||a*, Y||b, Z||c*)
 
  h = (02-21), r = 72 x 19 points
  h = (10-10), r = 72 x 19 points
  h = (10-11)(01-11), r = 72 x 19 points
  h = (10-12), r = 72 x 19 points
  h = (11-20), r = 72 x 19 points
  h = (11-21), r = 72 x 19 points
  h = (11-22), r = 72 x 19 points
 
odf3 = SO3FunRBF (Quartz → y↑→x)
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 5°
  center: 19848 orientations, resolution: 5°
  weight: 1

Modal Orientations

The modal orientation of an ODF is the crystallographic preferred orientation ori_pref of the texture. It is characterized as the maximum of the ODF. In MTEX it is returned as the second output argument of the command max

[~,ori_pref] = max(odf3)

ori_pref = orientation (Quartz → y↑→x)
 
  Bunge Euler angles in degree
     phi1     Phi    phi2
  133.047 34.5158  207.16

Lets mark this preferred orientation in the pole figures

plotPDF(odf3,pf.allH,'antipodal','superposition',pf.c);
annotate(ori_pref,'marker','s','MarkerFaceColor','black')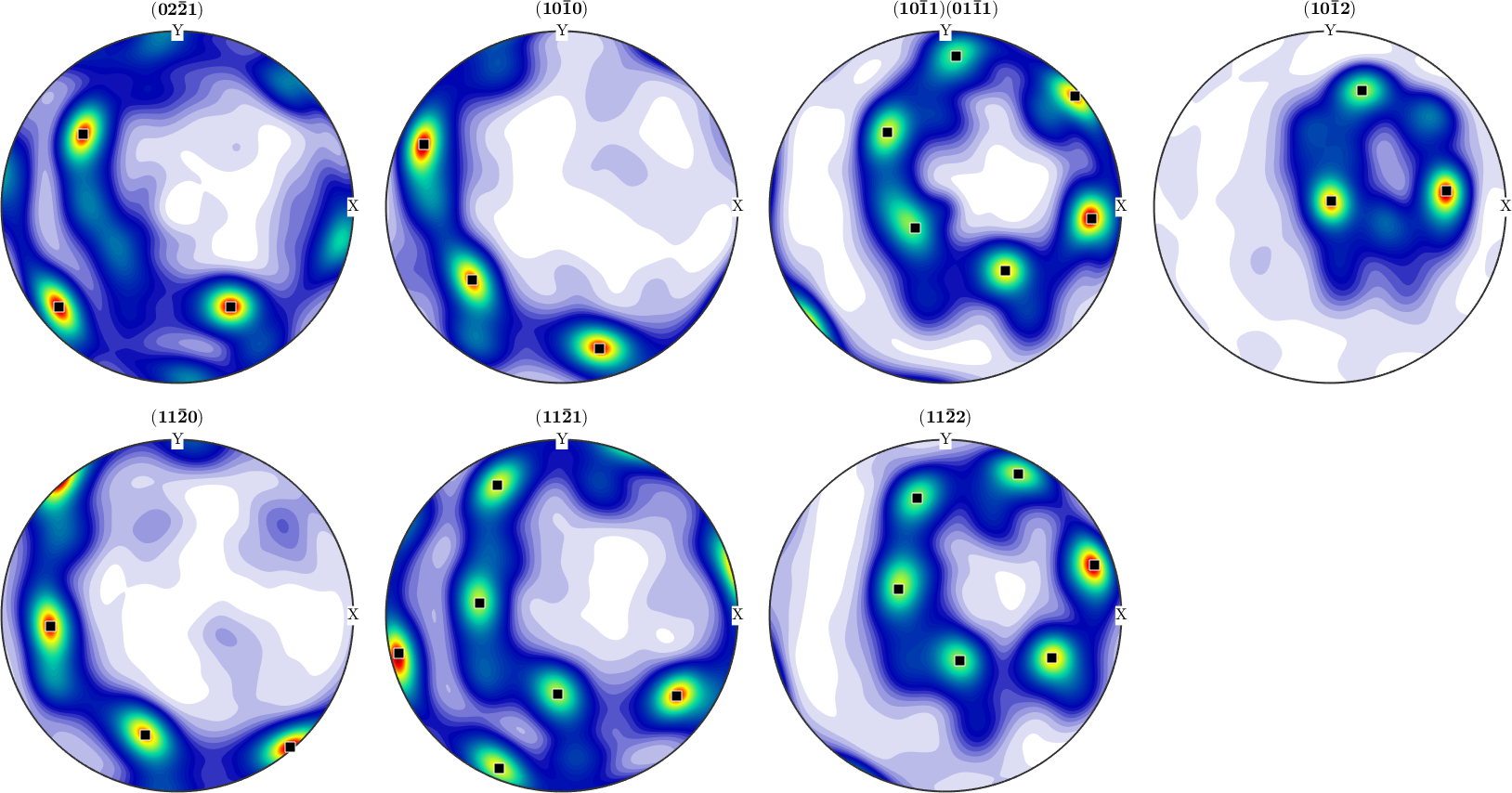

Texture Characteristics

Texture characteristics are used for a rough classification of ODFs into sharp and weak ones. The two most common texture characteristics are the entropy and the texture index. The texture index of an ODF $f$ is defined as:

$t = \int_{SO(3)} f({R})^2 dR$

We may either compute this integral using the command sum directly by

t = mean(odf1.*odf1)

t =
  288.5696

or, more efficiently, by the command norm

t = norm(odf1)^2

t =
  288.6802

The entropy of an ODF $f$ is defined as:

$H = - \int_{SO(3)} f({R}) \ln f({R}) dR$

H = entropy(odf2)

H =
   -2.8402

Volume Portions

Volume portions describes the relative volume of crystals having a certain orientation. The relative volume of crystals having a orientation close to a given orientation is computed by the command volume and the relative volume of crystals having a orientation close to a given fibre is computed by the command fibreVolume

The relative volume in percent of crystals with misorientation maximum 30 degree from the preferred orientation ori_pref:

V1 = volume(odf3, ori_pref, 30*degree) * 100

V1 =
   33.8649

The relative volume of crystals with misorientation maximum 20 degree from the preferred fibre in percent:

V2 = volume(odf2,f001_x,20*degree) * 100

V2 =
   95.1633