Bingham Distribution edit page

Theory

The Bingham distribution has the density function

\[ f(g;K,U) = _1\!F_1 \left(\frac{1}{2},2,K \right)^{-1} \exp \left\{ g^T UKU g \right\},\qquad g\in S^3, \]

where \(U\) is an \(4 \times 4\) orthogonal matrix with unit quaternions \(u_{1,..,4}\in S^3\) in the columns and \(K\) is a \(4 \times 4\) diagonal matrix with the entries \(k_1,..,k_4\) describing the shape of the distribution. \(_1F_1(\cdot,\cdot,\cdot)\) is the hypergeometric function with matrix argument normalizing the density.

The shape parameters \(k_1 \ge k_2 \ge k_3 \ge k_4\) give

  • a bipolar distribution, if \(k_1 + k_4 > k_2 + k_3\),
  • a circular distribution, if \(k_1 + k_4 = k_2 + k_3\),
  • a spherical distribution, if \(k_1 + k_4 < k_2 + k_3\),
  • a uniform distribution, if \(k_1 = k_2 = k_3 = k_4\),

The general setup of the Bingham distribution in MTEX is done as follows

cs = crystalSymmetry('1');

kappa = [100 90 80 0];   % shape parameters
U     = eye(4);          % orthogonal matrix

odf = BinghamODF(kappa,U,cs)
odf = SO3FunBingham (1 → xyz)
 
  kappa: 100 90 80 0
  weight: 1
h = [Miller(0,0,1,cs) Miller(1,0,0,cs) Miller(1,1,1,cs)];
plotzOutOfPlane
plotPDF(odf,h,'antipodal','silent');
plot(odf,'sections',6)

The bipolar case and unimodal distribution

First, we define some unimodal odf

odf_spherical = unimodalODF(orientation.rand(cs),'halfwidth',20*degree)
odf_spherical = SO3FunRBF (1 → xyz)
 
  unimodal component
  kernel: de la Vallee Poussin, halfwidth 20°
  center: 1 orientations
 
  Bunge Euler angles in degree
     phi1     Phi    phi2  weight
  191.522 82.7791 118.501       1
plotPDF(odf_spherical,h,'antipodal','silent')

Next, we simulate individual orientations from this odf, in a scattered axis/angle plot in which the simulated data looks like a sphere

ori_spherical = discreteSample(odf_spherical,1000);
close all
scatter(ori_spherical)

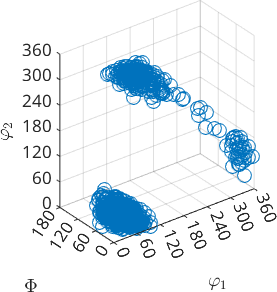
From this simulated EBSD data, we can estimate the parameters of the Bingham distribution,

odf_est = calcBinghamODF(ori_spherical)

plotPDF(odf_est,h,'antipodal','silent')
odf_est = SO3FunBingham (1 → xyz)
 
  kappa: 0 2 5.2 26
  weight: 1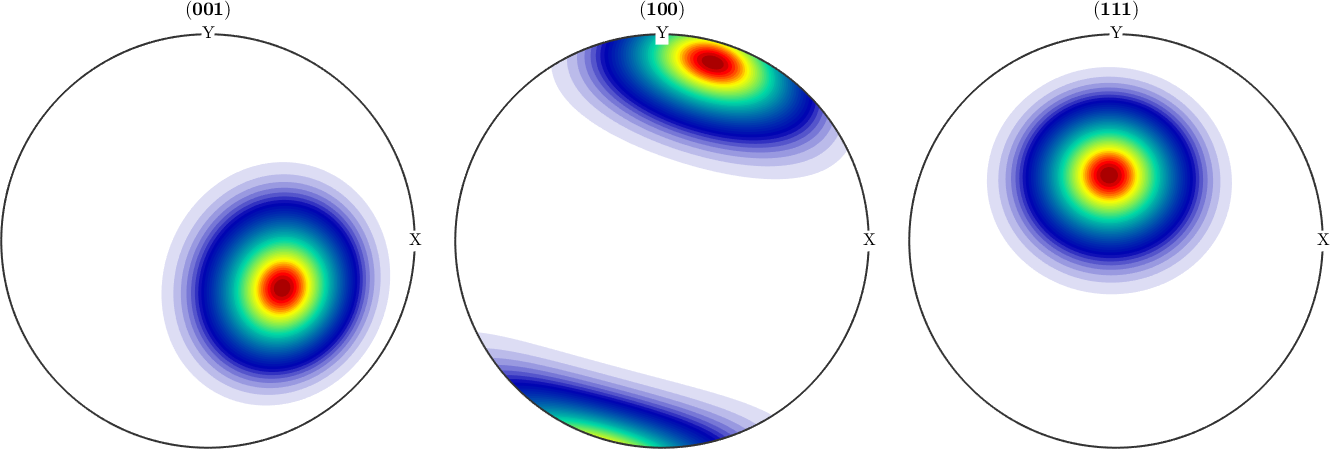

TODO

where U is the orthogonal matrix of eigenvectors of the orientation tensor and kappa the shape parameters associated with the U.

next, we test the different cases of the distribution on rejection

%T_spherical = bingham_test(ori_spherical,'spherical','approximated');
%T_oblate    = bingham_test(ori_spherical,'prolate',  'approximated');
%T_prolate   = bingham_test(ori_spherical,'oblate',   'approximated');

%t = [T_spherical T_oblate T_prolate]

The spherical test case failed to reject for some level of significance, hence we would dismiss the hypothesis prolate and oblate.

%df_spherical = BinghamODF(kappa,U,crystalSymmetry,specimenSymmetry)
%plotPDF(odf_spherical,h,'antipodal','silent')

Prolate case and fiber distribution

The prolate case corresponds to a fiber.

odf_prolate = fibreODF(Miller(0,0,1,crystalSymmetry('1')),zvector,...
  'halfwidth',20*degree)
odf_prolate = SO3FunCBF (1 → xyz)
 
  kernel: de la Vallee Poussin, halfwidth 20°
  fibre : (001) || 0,0,1
  weight: 1
plotPDF(odf_prolate,h,'upper','silent')

As before, we generate some random orientations from a model odf. The shape in an axis/angle scatter plot reminds of a cigar

ori_prolate = discreteSample(odf_prolate,1000);
close all
scatter(ori_prolate)

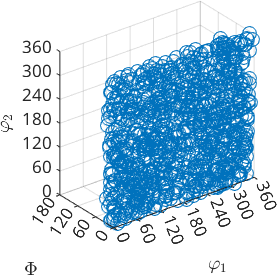
We estimate the parameters of the Bingham distribution

calcBinghamODF(ori_prolate)
ans = SO3FunBingham (1 → xyz)
 
  kappa: 0 6.6 50 51
  weight: 1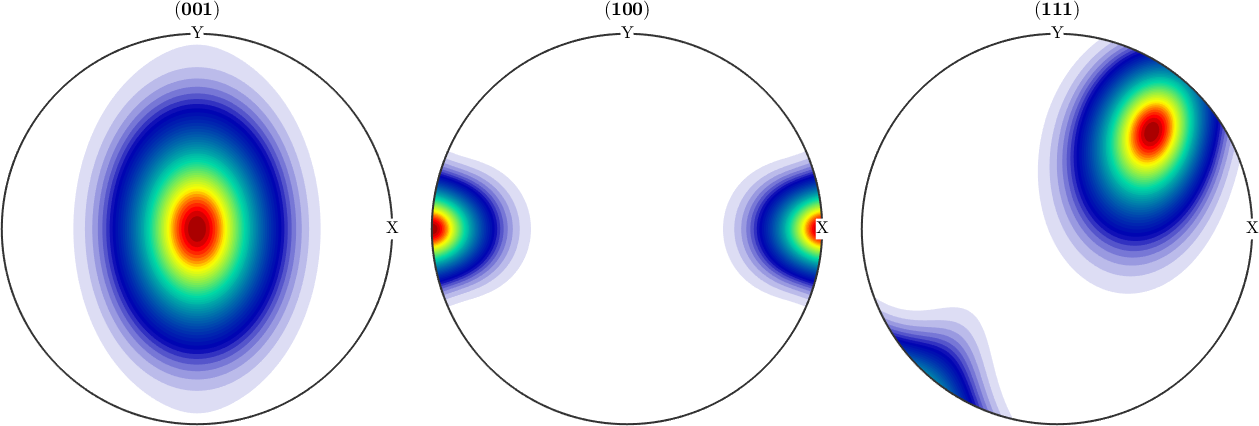

and test on the three cases

%T_spherical = bingham_test(ori_prolate,'spherical','approximated');
%T_oblate    = bingham_test(ori_prolate,'prolate',  'approximated');
%T_prolate   = bingham_test(ori_prolate,'oblate',   'approximated');

%t = [T_spherical T_oblate T_prolate]

The test clearly rejects the spherical and prolate case, but not the prolate. We construct the Bingham distribution from the parameters, it might show some skewness

odf_prolate = BinghamODF(kappa,U,crystalSymmetry,specimenSymmetry)
odf_prolate = SO3FunBingham (1 → xyz)
 
  kappa: 100 90 80 0
  weight: 1
plotPDF(odf_prolate,h,'antipodal','silent')

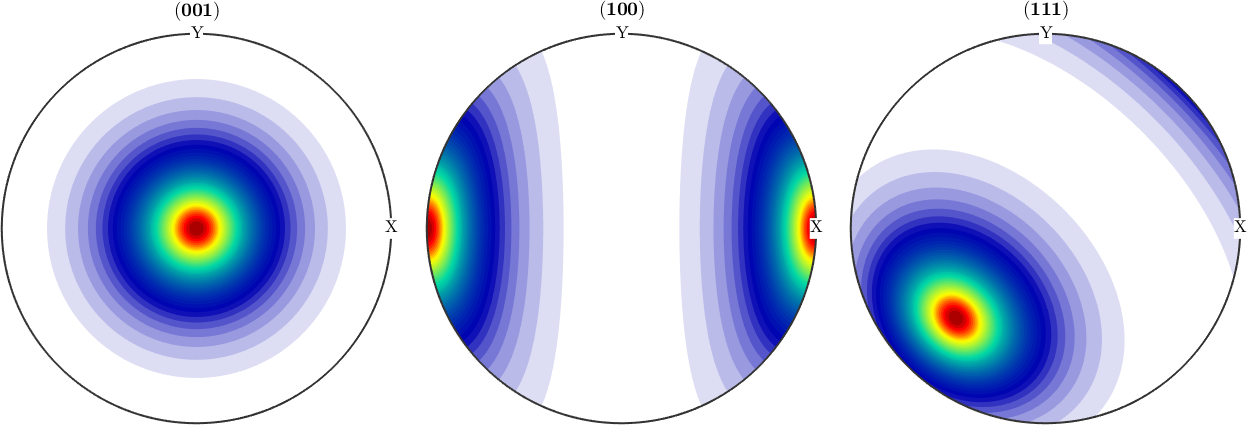
Oblate case

The oblate case of the Bingham distribution has no direct counterpart in terms of texture components, thus we can construct it straightforward

odf_oblate = BinghamODF([50 50 50 0],eye(4),crystalSymmetry,specimenSymmetry)
odf_oblate = SO3FunBingham (1 → xyz)
 
  kappa: 50 50 50 0
  weight: 1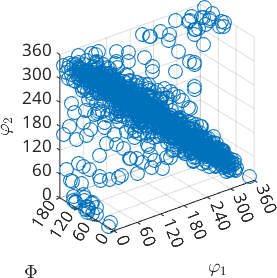
plotPDF(odf_oblate,h,'antipodal','silent')

The oblate cases in axis/angle space remind on a disk

ori_oblate = discreteSample(odf_oblate,1000);
close all
scatter(ori_oblate)

We estimate the parameters again

calcBinghamODF(ori_oblate)
ans = SO3FunBingham (1 → xyz)
 
  kappa: 0 54 54 55
  weight: 1

and do the tests

%T_spherical = bingham_test(ori_oblate,'spherical','approximated');
%T_oblate    = bingham_test(ori_oblate,'prolate',  'approximated');
%T_prolate   = bingham_test(ori_oblate,'oblate',   'approximated');

%t = [T_spherical T_oblate T_prolate]

the spherical and oblate case are clearly rejected, the prolate case failed to reject for some level of significance

odf_oblate = BinghamODF(kappa, U,crystalSymmetry,specimenSymmetry)
odf_oblate = SO3FunBingham (1 → xyz)
 
  kappa: 100 90 80 0
  weight: 1
plotPDF(odf_oblate,h,'antipodal','silent')

Bingham unimodal ODF 

% a modal orientation
cs = crystalSymmetry('-3m');
mod = orientation.byEuler(45*degree,0*degree,0*degree,cs);

% the corresponding Bingham ODF
odf = BinghamODF(20,mod)

plot(odf,'sections',6,'silent','contourf','sigma')
odf = SO3FunBingham (-3m1 → xyz)
 
  kappa: 20 0 0 0
  weight: 1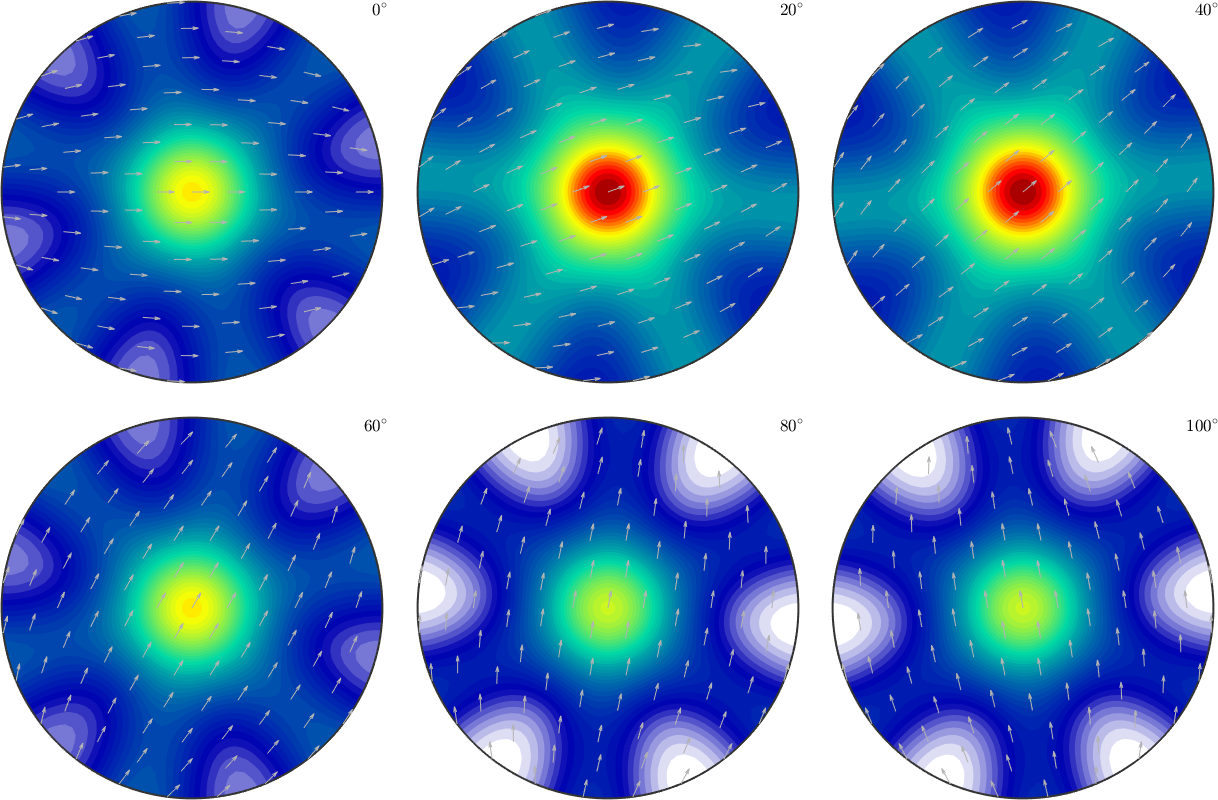

Bingham fibre ODF 

odf = BinghamODF([-10,-10,10,10],quaternion(eye(4)),cs)

plot(odf,'sections',6,'silent','sigma')
odf = SO3FunBingham (-3m1 → xyz)
 
  kappa: -10 -10 10 10
  weight: 1

Bingham spherical ODF 

odf = BinghamODF([-10,10,10,10],quaternion(eye(4)),cs)

plot(odf,'sections',6,'silent','sigma');
odf = SO3FunBingham (-3m1 → xyz)
 
  kappa: -10 10 10 10
  weight: 1