Sharp Color Keys

Sharp Color Keys edit page

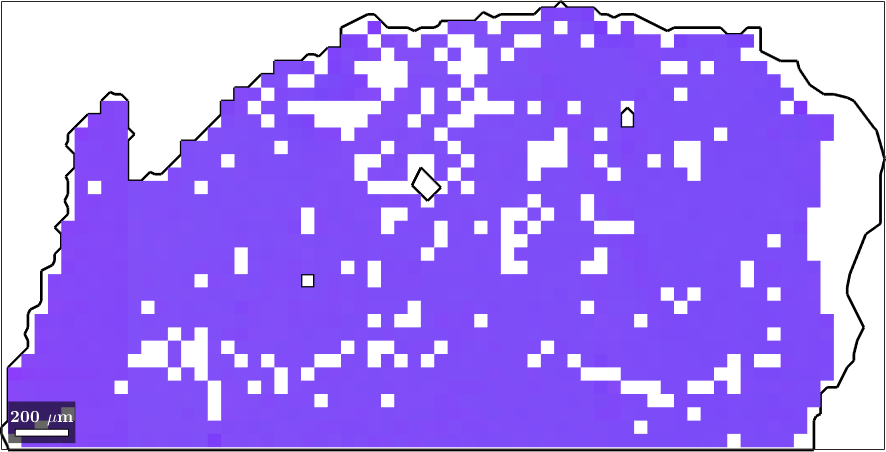
In this section we discuss color keys that are particular useful when analyzing data with very small deviation in orientation. Let us consider the following calcite data set

% plotting conventions
plotx2east, plotb2east
mtexdata sharp

ebsd = ebsd('calcite');

ipfKey = ipfColorKey(ebsd);

close all;
plot(ebsd,ipfKey.orientation2color(ebsd.orientations))

ebsd = EBSD
 
 Phase  Orientations     Mineral         Color  Symmetry  Crystal reference frame
     0    32 (0.16%)  notIndexed                                                 
     1  20119 (100%)     calcite  LightSkyBlue      -3m1       X||a*, Y||b, Z||c*
 
 Scan unit : um
 X x Y x Z : [0 200] x [-100 0] x [0 0]
 Normal vector: (0,0,1)

and have a look into the 101 inverse pole figure.

r = vector3d(1,0,1);

% compute the positions in the inverse pole figure
h = ebsd.orientations .\ r;
h = project2FundamentalRegion(h);

% compute the azimuth angle in degree
color = h.rho ./ degree;

plotIPDF(ebsd.orientations,r,'property',color,'MarkerSize',3,'grid')
mtexColorbar

I'm plotting 8333 random orientations out of 20119 given orientations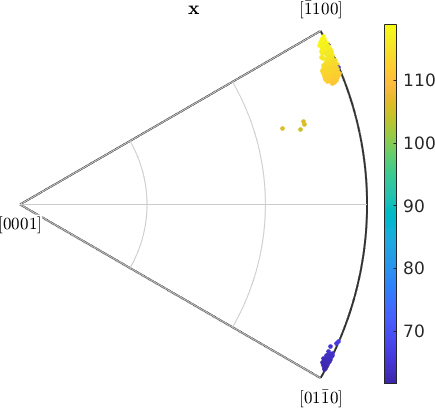

We see that all individual orientations are clustered around azimuth angle -20 degrees with some outliers at -35 degree. In order to increase the contrast for the main group, we restrict the color range from 110 degree to 120 degree.

setColorRange([-25 -15]);

% by the following lines we colorize the outliers in purple.
cmap = colormap;
cmap(end,:) = [1 0 1]; % make last color purple
cmap(1,:) = [1 0 1];   % make first color purple
colormap(cmap)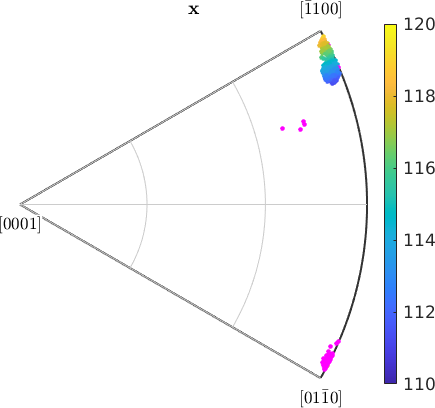

The same color coding we can now apply to the EBSD map.

% plot the data with the customized color
plot(ebsd,color)

% set scaling of the angles to 110 - 120 degree
setColorRange([-25 -15]);

% colorize outliers in purple.
cmap = colormap;
cmap(end,:) = [1 0 1];
cmap(1,:) = [1 0 1];
colormap(cmap)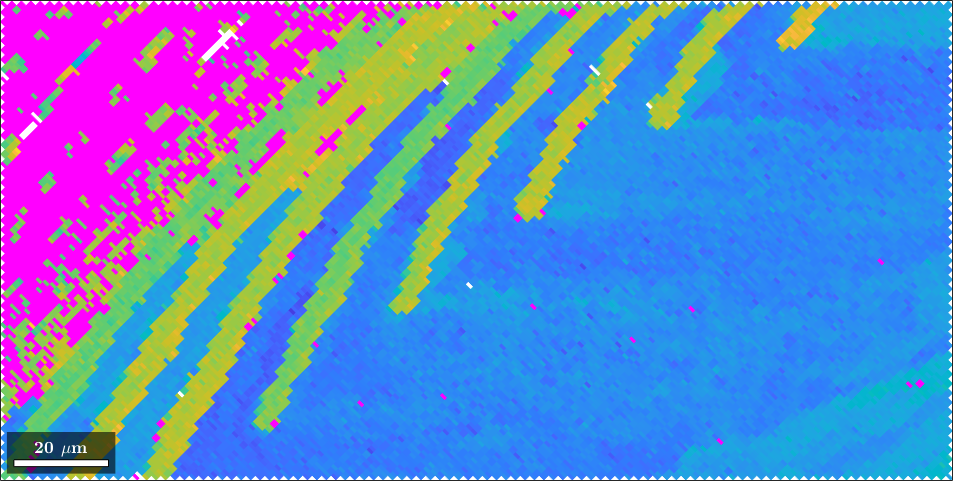

Sharpening the default color coding

Next, we want to apply the same ideas as above to the default MTEX color key, i.e. we want to stretch the colors such that they cover just the orientations of interest.

ipfKey = ipfHSVKey(ebsd.CS.properGroup);

% To this end, we first compute the inverse pole figure direction such that
% the mean orientation is just at the gray spot of the inverse pole figure
ipfKey.inversePoleFigureDirection = mean(ebsd.orientations,'robust') * ipfKey.whiteCenter;

close all;
plot(ebsd,ipfKey.orientation2color(ebsd.orientations))

We observe that the orientation map is almost completely gray, except for the outliers which appears black. Next, we use the option maxAngle to increase contrast in the grayish part

ipfKey.maxAngle = 7.5*degree;
plot(ebsd,ipfKey.orientation2color(ebsd.orientations))

You may play around with the option maxAngle to obtain better results. As for interpretation keep in mind that white color represents the mean orientation and the color becomes more saturated and later dark as the orientation to color diverges from the mean orientation.

Let's have a look at the corresponding color map.

plot(ipfKey,'resolution',0.25*degree)

% plot orientations into the color key
hold on
plotIPDF(ebsd.orientations,'points',10,'MarkerSize',1,'MarkerFaceColor','w','MarkerEdgeColor','w')
hold off

I'm plotting 10 random orientations out of 20119 given orientations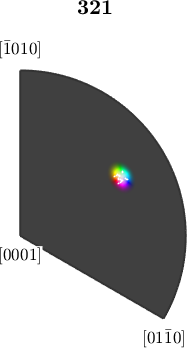

observe how in the inverse pole figure the orientations are scattered closely around the white center. Together with the fact that the transition from white to color is quite rapidly, this gives a high contrast.

The axis angle color key

A second option to visualize small orientation deviation, e.g. within a grains is the axis-angle color key. In order to demonstrate this color key let us first separate the EBSD into grains.

[grains,ebsd.grainId] = calcGrains(ebsd,'angle',1.5*degree);
ebsd(grains(grains.grainSize<=3)) = [];
[grains,ebsd.grainId] = calcGrains(ebsd,'angle',1.5*degree);

grains = smooth(grains,5);

In order to apply the @axisAngleColorKey we need to specify the crystal symmetry and a reference orientation oriRef. Often the meanorientation of the grains is a good choice.

ipfKey = axisAngleColorKey(ebsd('indexed'));

% use for the reference orientation the grain mean orientation
ipfKey.oriRef = grains.meanOrientation(ebsd.grainId);

plot(ebsd,ipfKey.orientation2color(ebsd.orientations))

hold on
plot(grains.boundary,'lineWidth',4)
hold off

Being able to visualize very small orientation changes gives us better way to observe how EBSD denoising methods work

F = halfQuadraticFilter;

ebsdS = smooth(ebsd,F,'fill',grains);

% use for the reference orientation the grain mean orientation
ipfKey.oriRef = grains.meanOrientation(ebsdS('indexed').grainId);

plot(ebsdS('indexed'),ipfKey.orientation2color(ebsdS('indexed').orientations))

hold on
plot(grains.boundary,'lineWidth',4)
hold off

Another example is when analyzing the orientation distribution within grains

mtexdata forsterite
ebsd = ebsd('indexed');

% segment grains
[grains,ebsd.grainId] = calcGrains(ebsd);

% find largest grains
largeGrains = grains(grains.grainSize > 800)

ebsd = ebsd(largeGrains(1))

ebsd = EBSD
 
 Phase  Orientations     Mineral         Color  Symmetry  Crystal reference frame
     0   58485 (24%)  notIndexed                                                 
     1  152345 (62%)  Forsterite  LightSkyBlue       mmm                         
     2   26058 (11%)   Enstatite  DarkSeaGreen       mmm                         
     3   9064 (3.7%)    Diopside     Goldenrod     12/m1       X||a*, Y||b*, Z||c
 
 Properties: bands, bc, bs, error, mad
 Scan unit : um
 X x Y x Z : [0 36550] x [0 16750] x [0 0]
 Normal vector: (0,0,1)
 
 
largeGrains = grain2d
 
 Phase  Grains  Pixels     Mineral  Symmetry  Crystal reference frame
     1      56   85514  Forsterite       mmm                         
     2       2    1969   Enstatite       mmm                         
 
 boundary segments: 17904 (812029 µm)
 inner boundary segments: 222 (10022 µm)
 triple points: 1247
 
 Properties: meanRotation, GOS
 
 
ebsd = EBSD
 
 Phase  Orientations     Mineral         Color  Symmetry  Crystal reference frame
     1   1453 (100%)  Forsterite  LightSkyBlue       mmm                         
 
 Properties: bands, bc, bs, error, mad, grainId
 Scan unit : um
 X x Y x Z : [14800 17850] x [0 1600] x [0 0]
 Normal vector: (0,0,1)

When plotting one specific grain with its orientations we see that they all are very similar and, hence, get the same color

% plot a grain
close all
plot(largeGrains(1).boundary,'linewidth',2)
hold on
plot(ebsd,ebsd.orientations)
hold off

when applying the option sharp MTEX colors the mean orientation as white and scales the maximum saturation to fit the maximum misorientation angle. This way deviations of the orientation within one grain can be visualized.

% plot a grain
plot(largeGrains(1).boundary,'linewidth',2)
hold on
ipfKey = ipfHSVKey(ebsd);
ipfKey.inversePoleFigureDirection = mean(ebsd.orientations) * ipfKey.whiteCenter;
ipfKey.maxAngle = 2*degree;
plot(ebsd,ipfKey.orientation2color(ebsd.orientations))
hold off