Theory
For an orientation distribution function (ODF) \(f \colon \mathrm{SO}(3) \to R\) the inverse pole density function \(P_{\vec r}\) with respect to a fixed specimen direction \(\vec r\) is spherical function defined as the integral
\[ P_{\vec r}(\vec h) = \int_{g \vec h = \vec r} f(g) dg \]
The pole density function \(P_{\vec r}(\vec h)\) evaluated at a crystal direction \(\vec h\) can be interpreted as the volume percentage of crystals with the crystal lattice planes \(\vec h\) beeing normal to the specimen direction \(\vec r\).
In order to illustrate the concept of inverse pole figures at an example lets us first define a model ODF to be plotted later on.
cs = crystalSymmetry('32');
mod1 = orientation.byEuler(90*degree,40*degree,110*degree,'ZYZ',cs);
mod2 = orientation.byEuler(50*degree,30*degree,-30*degree,'ZYZ',cs);
odf = 0.2*unimodalODF(mod1) ...
+ 0.3*unimodalODF(mod2) ...
+ 0.5*fibreODF(Miller(0,0,1,cs),vector3d(1,0,0),'halfwidth',10*degree)
%odf = 0.2*unimodalODF(mod2)odf = SO3FunComposition (321 → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 10°
center: 2 orientations
Bunge Euler angles in degree
phi1 Phi phi2 weight
180 40 20 0.2
140 30 240 0.3
fibre component
kernel: de la Vallee Poussin, halfwidth 10°
fibre : (0001) || 1,0,0
weight: 0.5and lets switch to the LaboTex colormap
setMTEXpref('defaultColorMap',LaboTeXColorMap);
% Plotting inverse pole figures is analogously to plotting pole figures
% with the only difference that you have to use the command
% <SO3Fun.plotIPDF.html plotIPDF> and you to specify specimen directions and
% not crystal directions.
plotIPDF(odf,[xvector,zvector])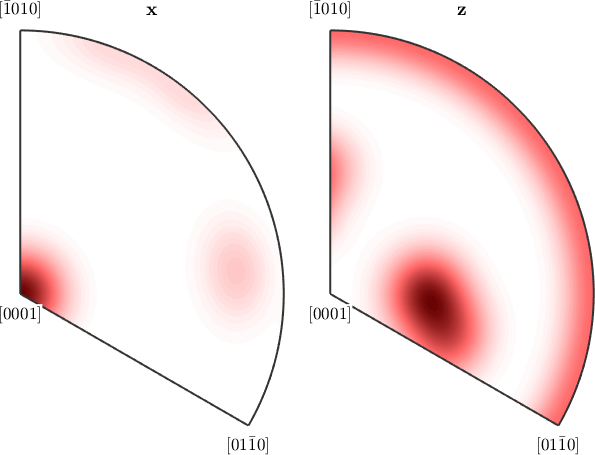
Imposing antipodal symmetry to the inverse pole figures halfes the fundamental region
plotIPDF(odf,[xvector,zvector],'antipodal')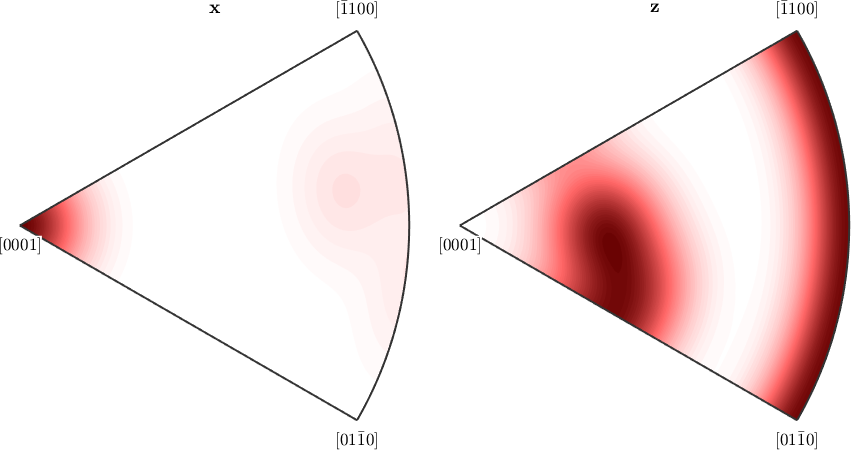
By default MTEX always plots only the fundamental region with respect to the crystal symmetry. In order to plot the complete inverse pole figure you have to use the option complete.
plotIPDF(odf,[xvector,zvector],'complete','upper')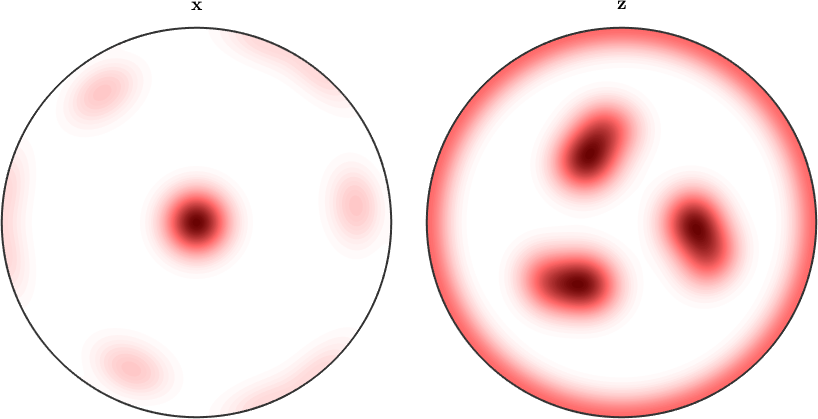
This illustrates also more clearly the effect of the antipodal symmetry
plotIPDF(odf,[xvector,zvector],'complete','antipodal','upper')
Finally, lets set back the default colormap.
setMTEXpref('defaultColorMap',WhiteJetColorMap);