In many usecases one is interested in grid of orientations that somehow uniformely cover the orientation space. The simplest way of generating equispaced orientations with given resolution is by the command
% define a crystal symmetry
cs = crystalSymmetry('432')
% define a grid of orientations
ori = equispacedSO3Grid(cs,'resolution',5*degree)cs = crystalSymmetry
symmetry: 432
elements: 24
a, b, c : 1, 1, 1
ori = SO3Grid (432 → y↑→x)
grid: 4958 orientations, resolution: 5°Lets visualize them
plot(ori,'axisAngle')plot 2000 random orientations out of 4958 given orientations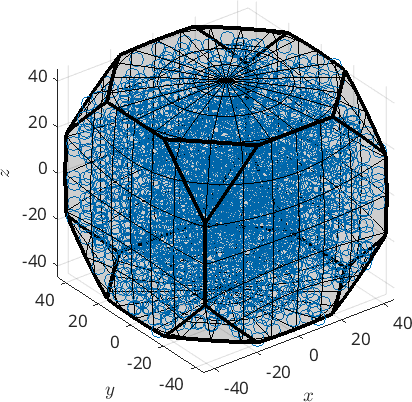
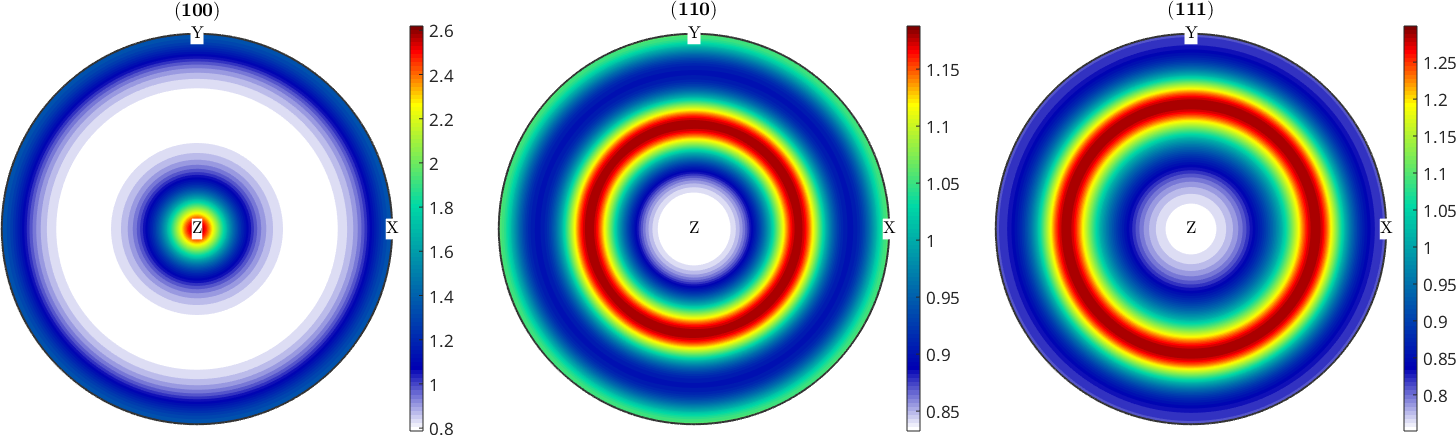
Check for equidistribution
odf = unimodalODF(ori)
plotPDF(odf,Miller({1,0,0},{1,1,0},{1,1,1},cs))
mtexColorbarodf = SO3FunRBF (432 → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 10°
center: 4958 orientations, resolution: 5°
weight: 1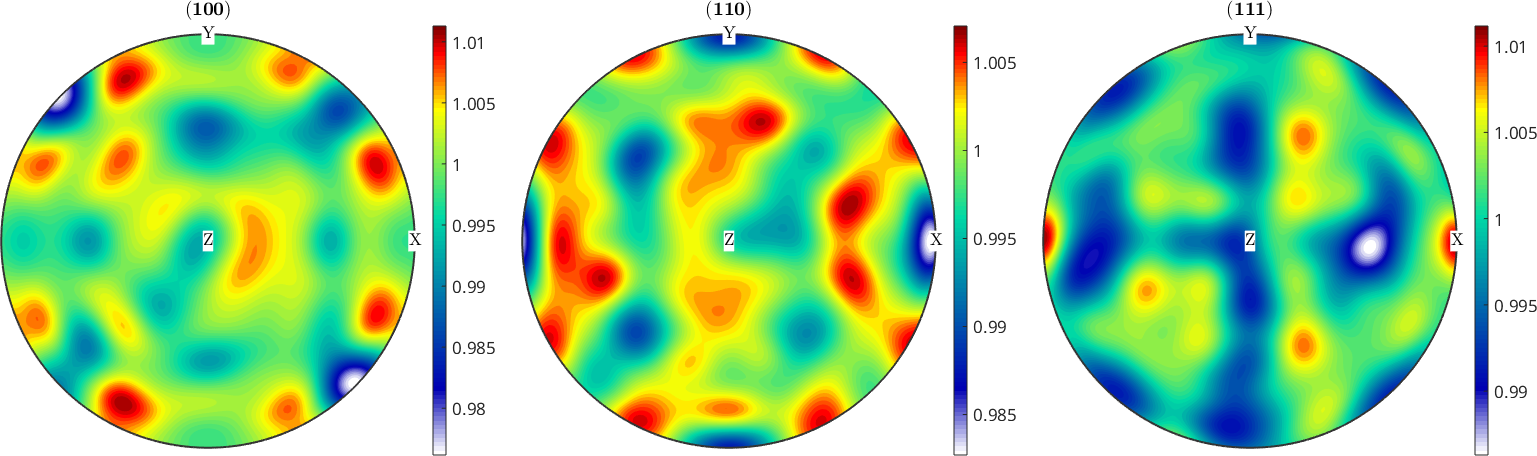
ori = regularSO3Grid(cs,'resolution',5*degree)ori = orientation (432 → y↑→x)
size: 72 x 19 x 18plot(ori,'axisAngle')plot 2000 random orientations out of 24624 given orientations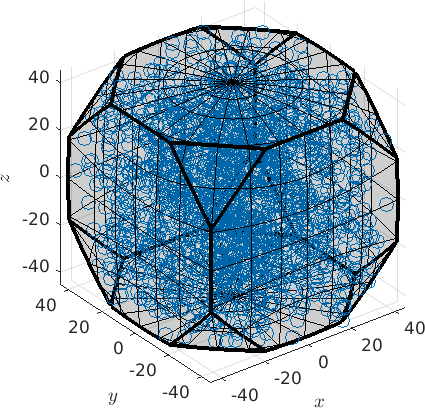
odf = unimodalODF(ori)
plotPDF(odf,Miller({1,0,0},{1,1,0},{1,1,1},cs))
mtexColorbarodf = SO3FunRBF (432 → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 10°
center: 24624 orientations