Simulating pole figure data from a given ODF is useful to investigate pole figure to ODF reconstruction routines. Let us start with a model ODF given as the superposition of 6 components.
cs = crystalSymmetry('orthorhombic');
mod1 = orientation.byAxisAngle(xvector,45*degree,cs);
mod2 = orientation.byAxisAngle(yvector,65*degree,cs);
model_odf = 0.5*uniformODF(cs) + ...
0.05*fibreODF(Miller(1,0,0,cs),xvector,'halfwidth',10*degree) + ...
0.05*fibreODF(Miller(0,1,0,cs),yvector,'halfwidth',10*degree) + ...
0.05*fibreODF(Miller(0,0,1,cs),zvector,'halfwidth',10*degree) + ...
0.05*unimodalODF(mod1,'halfwidth',15*degree) + ...
0.3*unimodalODF(mod2,'halfwidth',25*degree);plot(model_odf,'sections',6,'silent','sigma')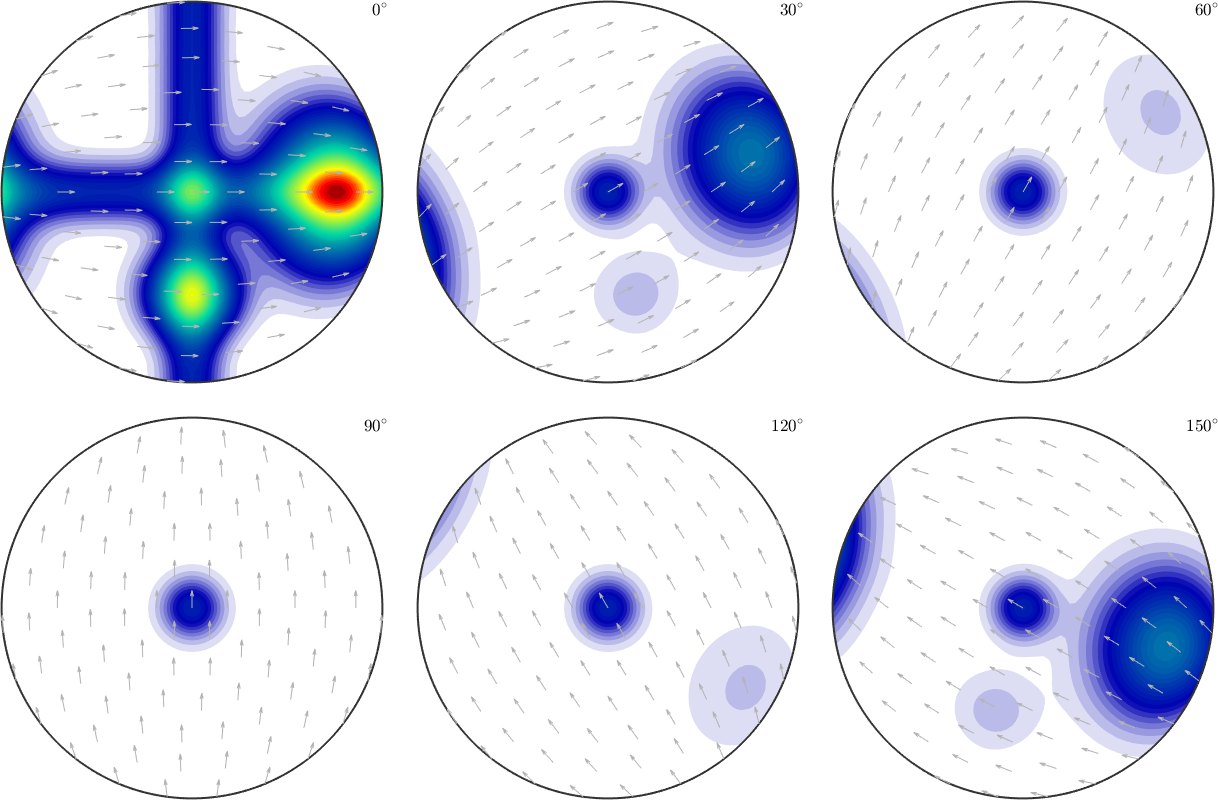
In order to simulate pole figure data, the following parameters have to be specified
- an arbitrary ODF
- a list of Miller indices
- a grid of specimen directions
- superposition coefficients (optional)
- the magnitude of error (optional)
The list of Miller indices
h = [Miller(1,1,1,cs),Miller(1,1,0,cs),Miller(1,0,1,cs),Miller(0,1,1,cs),...
Miller(1,0,0,cs),Miller(0,1,0,cs),Miller(0,0,1,cs)];The grid of specimen directions
r = regularS2Grid('resolution',5*degree);Now the pole figures can be simulated using the command calcPoleFigure.
pf = calcPoleFigure(model_odf,h,r)pf = PoleFigure (y↑→x)
crystal symmetry : mmm
h = (111), r = 72 x 37 points
h = (110), r = 72 x 37 points
h = (101), r = 72 x 37 points
h = (011), r = 72 x 37 points
h = (100), r = 72 x 37 points
h = (010), r = 72 x 37 points
h = (001), r = 72 x 37 pointsAdd some noise to the data. Here we assume that the mean intensity is 1000.
pf = noisepf(pf,1000);Plot the simulated pole figures.
plot(pf)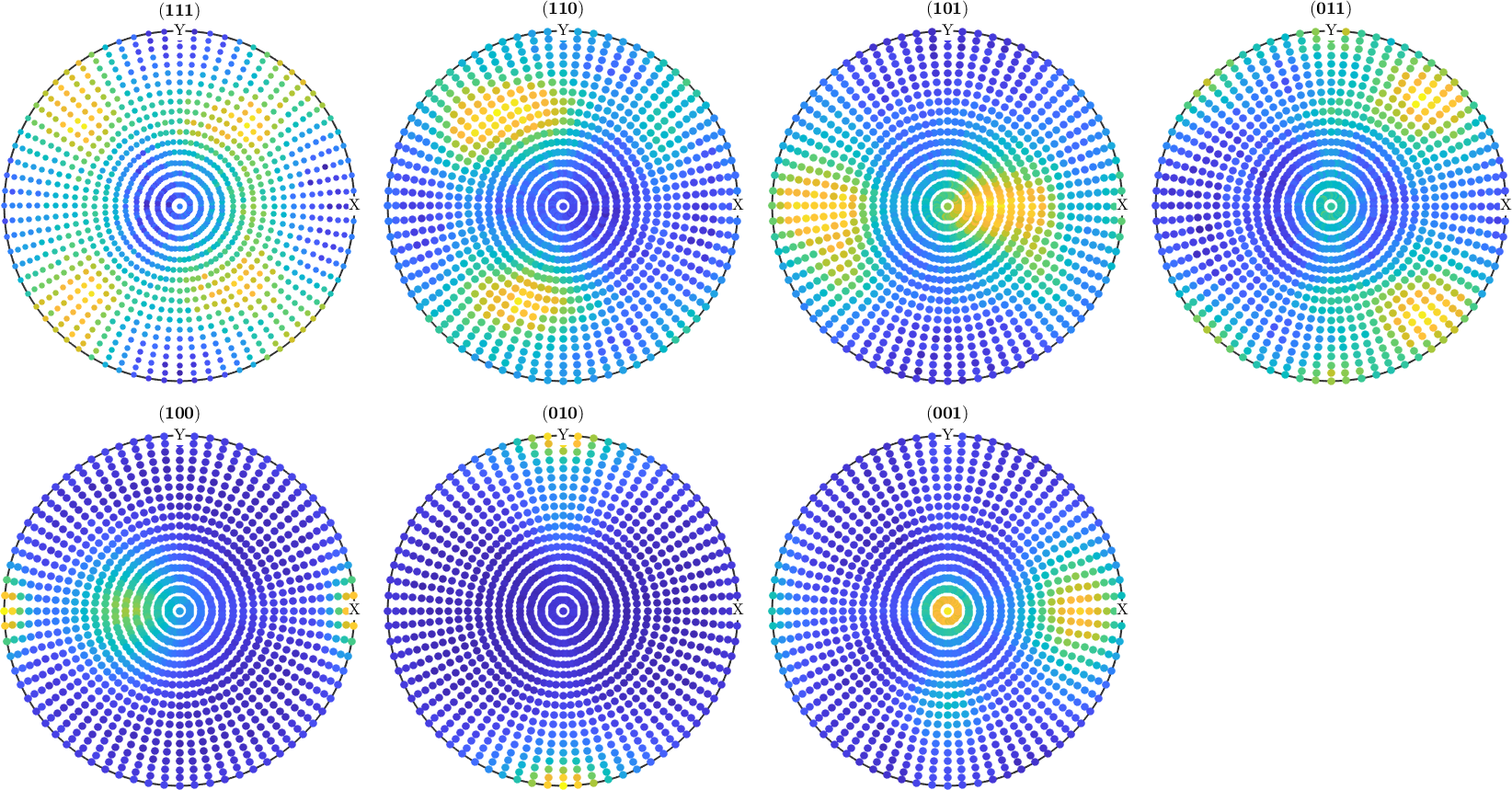
ODF Estimation from Pole Figure Data
From these simulated pole figures we can now estimate an ODF,
odf = calcODF(pf)odf = SO3FunRBF (mmm → y↑→x)
uniform component
weight: 0.47
multimodal components
kernel: de la Vallee Poussin, halfwidth 5°
center: 29772 orientations, resolution: 5°
weight: 0.53which can be plotted,
plot(odf,'sections',6,'silent','sigma')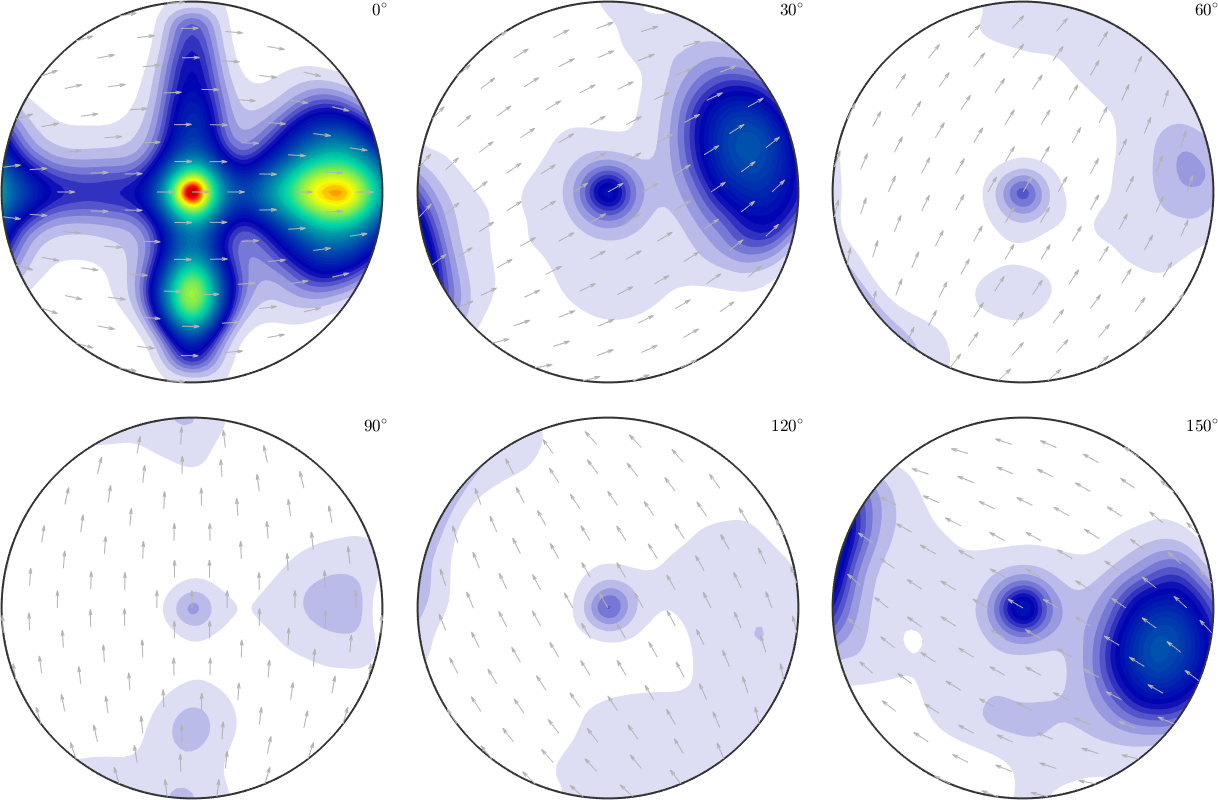
and compared to the original model ODF.
calcError(odf,model_odf,'resolution',5*degree)ans =
0.0836Exploration of the relationship between estimation error and number of pole figures
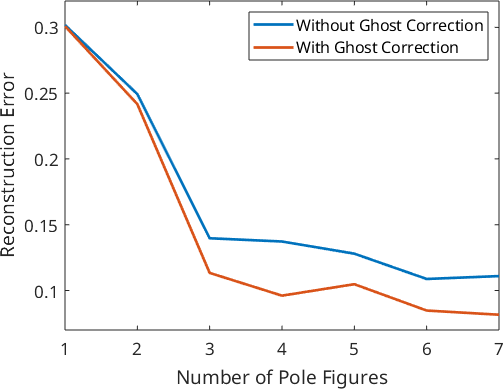
For a more systematic analysis of the estimation error, we vary the number of pole figures used for ODF estimation from 1 to 7 and calculate for any number of pole figures the approximation error. Furthermore, we also apply ghost correction and compare the approximation error to the previous reconstructions.
e = [];
for i = 1:pf.numPF
odf = calcODF(pf({1:i}),'silent','NoGhostCorrection');
e(i,1) = calcError(odf,model_odf,'resolution',2.5*degree);
odf = calcODF(pf({1:i}),'silent');
e(i,2) = calcError(odf,model_odf,'resolution',2.5*degree);
endPlot the error in dependency of the number of single orientations.
close all;
plot(1:pf.numPF,e,'LineWidth',2)
ylim([0.07 0.32])
xlabel('Number of Pole Figures');
ylabel('Reconstruction Error');
legend({'Without Ghost Correction','With Ghost Correction'});