In MTEX we describe radial basis functions on the rotation group \(SO(3)\) by the class SO3FunRBF.
This includes the following three types of ODFs.
The Uniform ODF
The uniform ODF
\[f(g) = 1,\quad g \in SO(3),\]
is everywhere identical to one. In order to define a uniform ODF one needs only to specify its crystal and specimen symmetry and to use the command uniformODF.
cs = crystalSymmetry('cubic');
ss = specimenSymmetry('orthorhombic');
odf = uniformODF(cs,ss)odf = SO3FunRBF (m-3m → y↑→x (mmm))
uniform component
weight: 1Unimodal ODFs
An unimodal ODF
\[f(g; x) = \psi (\angle(g,x)),\quad g \in SO(3),\]
is specified by a radial symmetrical function \(\psi\) centered at a modal orientation, \(x\in SO(3)\). In order to define a unimodal ODF one needs
- a preferred orientation mod1
- a kernel function
psidefining the shape - the crystal symmetry
cs = crystalSymmetry('432');
ori = orientation.byMiller([1,2,2],[2,2,1],cs);
psi = SO3vonMisesFisherKernel('halfwidth',10*degree);
odf1 = unimodalODF(ori,psi)
plotPDF(odf1,[Miller(1,0,0,cs),Miller(1,1,0,cs)],'antipodal')odf1 = SO3FunRBF (432 → y↑→x)
unimodal component
kernel: van Mises Fisher, halfwidth 10°
center: 1 orientations
Bunge Euler angles in degree
phi1 Phi phi2 weight
116.565 48.1897 26.5651 1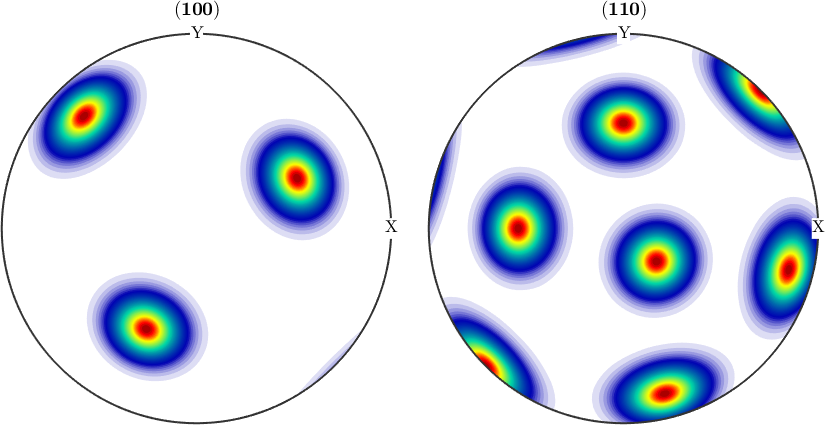
For simplicity one can also omit the kernel function. In this case the default SO(3) de la Vallee Poussin kernel is chosen with half width of 10 degree.
Multimodal ODFs
We define a second unimodal ODF with same kernel function and same crystal symmetry at an other orientation.
ori2 = orientation.byMiller([1,1,2],[0,2,1],cs)
odf2 = unimodalODF(ori2,psi)
plotPDF(odf2,[Miller(1,0,0,cs),Miller(1,1,0,cs)],'antipodal')ori2 = orientation (432 → y↑→x)
Bunge Euler angles in degree
phi1 Phi phi2
309.232 35.2644 45
odf2 = SO3FunRBF (432 → y↑→x)
unimodal component
kernel: van Mises Fisher, halfwidth 10°
center: 1 orientations
Bunge Euler angles in degree
phi1 Phi phi2 weight
309.232 35.2644 45 1
By adding this unimodal ODFs we get an so called multimodal ODF, which by construction is the sum of the radial symmetrical function \(\psi\) centered at some orientations.
odf3 = odf1 + odf2
plotPDF(odf3,[Miller(1,0,0,cs),Miller(1,1,0,cs)],'antipodal')odf3 = SO3FunRBF (432 → y↑→x)
multimodal components
kernel: van Mises Fisher, halfwidth 10°
center: 2 orientations
Bunge Euler angles in degree
phi1 Phi phi2 weight
116.565 48.1897 26.5651 1
309.232 35.2644 45 1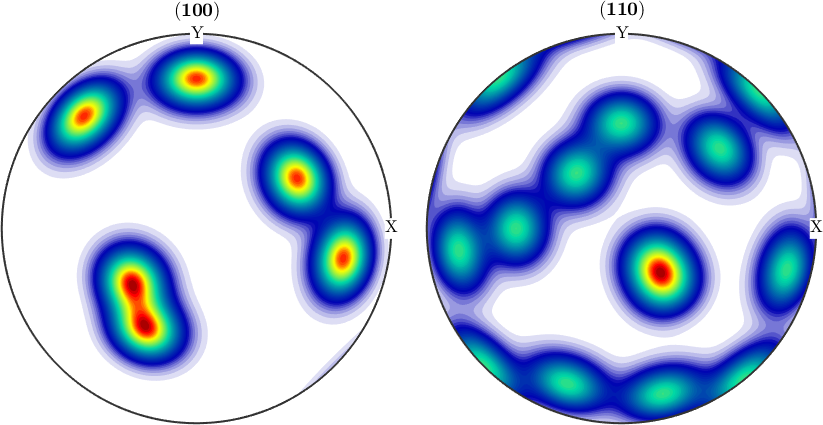
Its also possible to define an multimodal ODF by more than two orientations, for example
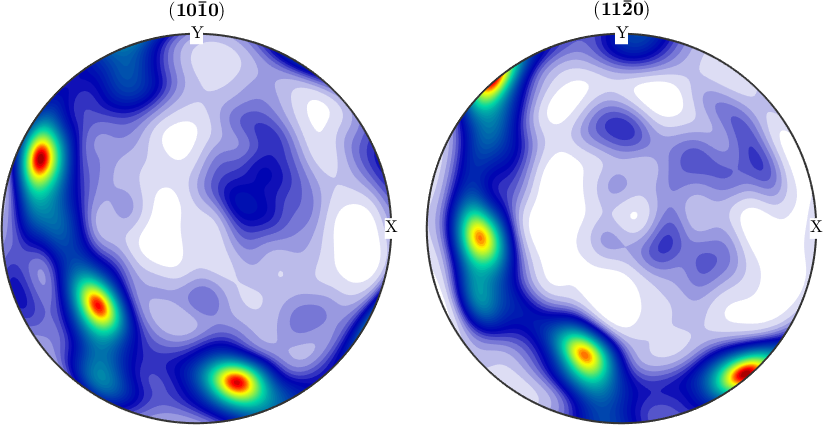
odf4 = SO3FunRBF.example
plotPDF(odf4,[Miller(1,0,0,odf4.CS),Miller(1,1,0,odf4.CS)],'antipodal')odf4 = SO3FunRBF (-3m1 → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 5°
center: 19848 orientations, resolution: 5°
weight: 1