Spherical Functions

By a variable of type S2Fun it is possible to represent an entire function on the two dimensional sphere. A typical example of such a function is the pole density function of a given ODF with respect to a fixed crystal direction.

% the famouse Santa Fe orientation distribution function
odf = SantaFe;

% the (100) pole density function
pdf = odf.calcPDF(Miller(1,0,0,odf.CS))

pdf = S2FunHarmonicSym (xyz (222))
  bandwidth: 25
  antipodal: true
  isReal: true

Since, the variable pdf stores all information about this function we may evaluate it for any direction r

% take a random direction
r = vector3d.rand;

% and evaluate the pdf at this direction
pdf.eval(r)

ans =
    1.2316

We may also plot the function in any spherical projection

plot(pdf)

or find its local maxima

[~,localMax] = max(pdf,'numLocal',12)

annotate(localMax)

localMax = vector3d
 size: 6 x 1
 antipodal: true
         x        y        z
  0.665345 0.338549 0.665357
  0.665333 0.665372 0.338544
  0.338446 0.665332 0.665423
         0        1        0
         1        0        0
         0        0        1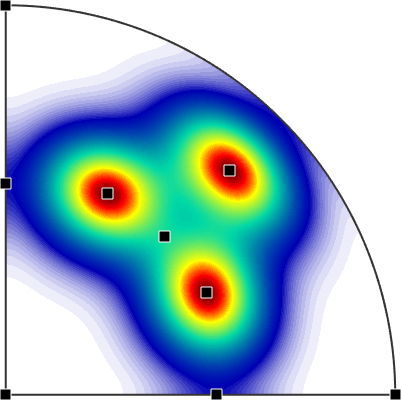

A complete list of operations that can be performed with spherical functions can be found in section Operations.

Representation of Spherical Functions

In MTEX there exist different ways for representing spherical functions internally.

All representations allow for the same operations which are specified for the abstact class S2Fun. In particular it is possible to calculate with spherical functions as with ordinary numbers, i.e., you can add, multiply arbitrary functions, take the mean, integrate them or compute gradients.

Generalizations of Spherical Functions