Defining Three Dimensional Vectors

Three dimensional vectors in the Euclidean space are represented by variables of the class vector3d.

Cartesian Coordinates

The standard way to define specimen directions is by its x, y and z coordinates.

v = vector3d(1,2,3)

v = vector3d
  x y z
  1 2 3

This gives a single vector with coordinates (1,1,0) with respect to the X, Y, Z coordinate system. Lets visualize this vector

plot(v)
annotate([vector3d.X,vector3d.Y,vector3d.Z],'label',{'X','Y','Z'},'backgroundcolor','w')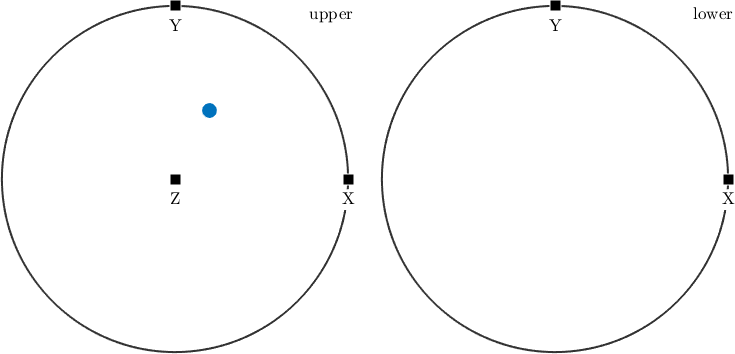

Note that the alignment of the X, Y, Z axes is only a plotting convention, which can be easily changed without changing the coordinates, e.g., by setting

plotx2north
plot(v,'grid')
annotate([vector3d.X,vector3d.Y,vector3d.Z],'label',{'X','Y','Z'},'backgroundcolor','w')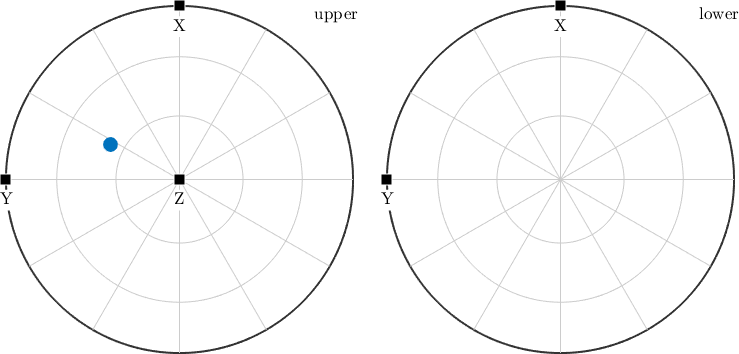

One can easily access the coordinates of any vector by

v.x

ans =
     1

or change it by

v.x = 0

v = vector3d
  x y z
  0 2 3

Polar Coordinates

A second way to define specimen directions is by polar coordinates, i.e. by its polar angle and its azimuth angle. This is done by the option polar.

polar_angle = 60*degree;
azimuth_angle = 45*degree;
v = vector3d.byPolar(polar_angle,azimuth_angle)

plotx2east
plot(v,'grid')
annotate([vector3d.X,vector3d.Y,vector3d.Z],'label',{'X','Y','Z'},'backgroundcolor','w')

v = vector3d
         x        y        z
  0.612372 0.612372      0.5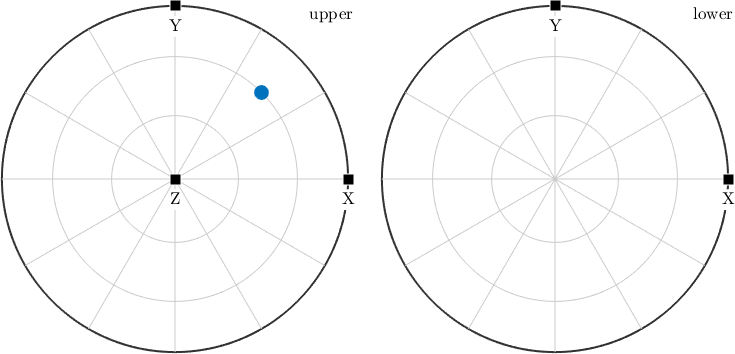

Analogously as for the Cartesian coordinates we can access and change polar coordinates directly by

v.rho ./ degree   % the azimuth angle in degree
v.theta ./ degree % the polar angle in degree

ans =
   45.0000
ans =
   60.0000