Slip Transmission edit page

How to analyze slip transmission at grain boundaries

Import Titanium data

From Mercier D. - MTEX 2016 Workshop - TU Chemnitz (Germany) Calculation and plot on GBs of m' parameter Dataset from Mercier D. - cp-Ti (alpha phase - hcp)

mtexdata csl

% compute grains
[grains, ebsd.grainId] = calcGrains(ebsd('indexed'));

% make them a bit nicer
grains = smooth(grains);

% extract inner phase grain boundaries
gB = grains.boundary('indexed');

plot(ebsd,ebsd.orientations)
hold on
plot(grains.boundary)
hold off
ebsd = EBSD
 
 Phase   Orientations  Mineral         Color  Symmetry  Crystal reference frame
    -1  154107 (100%)     iron  LightSkyBlue      m-3m                         
 
 Properties: ci, error, iq
 Scan unit : um
 X x Y x Z : [0 511] x [0 300] x [0 0]
 Normal vector: (0,0,1)

Taylor model

% consider Basal slip
sS = slipSystem.fcc(ebsd.CS)

% and all symmetrically equivalent variants
sS = sS.symmetrise;

% consider plane strain
q = 0.5;
eps = strainTensor(diag([-q 1 -(1-q)]));

% and compute Taylor factor as well as the active slip systems
[M,b,W] = calcTaylor(inv(grains.meanOrientation).*eps,sS);
sS = slipSystem (iron)
 
  u    v    w  | h    k    l CRSS
  0    1   -1    1    1    1    1
% find the maximum
[~,id] = max(b,[],2);

The variable id contains now for each grain the id of the slip system with the largest Schmidt factor. In order to visualize it we first rotate for each grain the slip system with largest Schmid factor in specimen coordinates

sSGrain = grains.meanOrientation .* sS(id)

% and plot then the plane normal and the Burgers vectors into the centers
% of the grains

plot(grains,M)

largeGrains = grains(grains.grainSize > 10)

hold on
quiver(grains,sSGrain.trace,'displayName','slip plane trace')
hold on
quiver(grains,sSGrain.b,'displayName','slip direction','project2plane')
hold off

legend show
sSGrain = slipSystem (xyz)
 CRSS: 1
 size: 885 x 1
 
 
largeGrains = grain2d
 
 Phase  Grains  Pixels  Mineral  Symmetry  Crystal reference frame
    -1     442  153261     iron      m-3m                         
 
 boundary segments: 23355 (19528 µm)
 inner boundary segments: 93 (82 µm)
 triple points: 1444
 
 Properties: meanRotation, GOS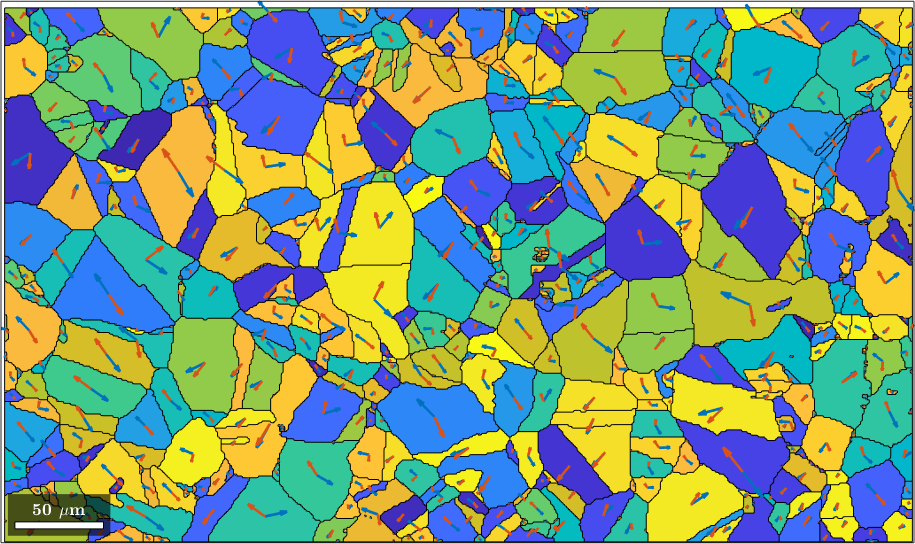

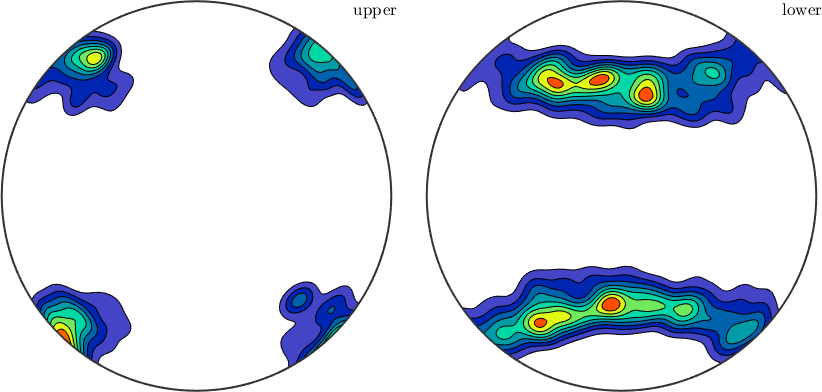
We may also analyze the distribution of the slip directions in a pole figure plot

plot(sSGrain.b)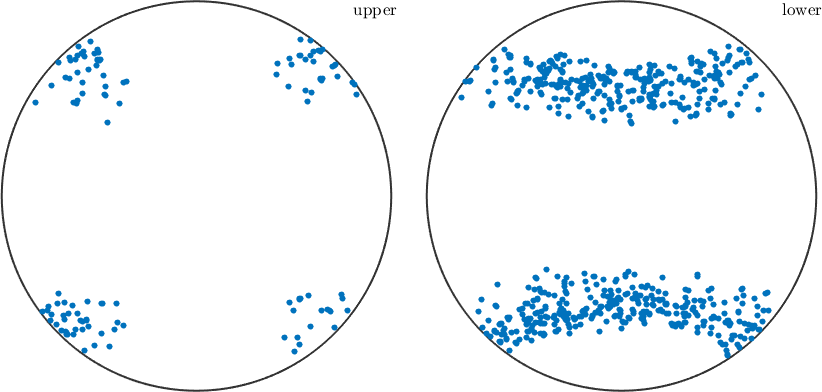

The same as a contour plot. We see a clear trend towards east.

plot(sSGrain.b,'contourf')