Inverse Pole Figure Color Coding of Orientation Maps

Inverse Pole Figure Color Coding of Orientation Maps edit page

This sections explains how to colorize orientation maps. The mathematics behind the default MTEX color key is explained in detail in the paper Orientations - perfectly colored.

Let us first import some sample EBSD data. We shall do this at the example of olivine data.

mtexdata olivine
ebsd('olivine').CS = ebsd('olivine').CS.Laue;

ebsd = EBSD
 
 Phase  Orientations       Mineral         Color  Symmetry  Crystal reference frame
     1   44953 (90%)       olivine  LightSkyBlue       222                         
     2   1370 (2.8%)      Dolomite  DarkSeaGreen         3       X||a, Y||b*, Z||c*
     3   2311 (4.6%)     Enstatite     Goldenrod       222                         
     4   1095 (2.2%)  Chalcopyrite    LightCoral       422                         
 
 Properties: ci, fit, iq, sem_signal, unknown1, unknown2, unknown3, unknown4, oldId
 Scan unit : um
 X x Y x Z : [0 888] x [-888 0] x [-1.1e-13 0]
 Normal vector: (0,0,1)

In order to illustrate the orientations of the olivine crystals we first define the habitus of a olivine crystal

cS = crystalShape.olivine;

plot(cS,'colored')

Next we represent the orientation of each grain by an appropriately rotated crystal. This is done by the following commands

% 1. reconstruct the grains
[grains,ebsd.grainId] = calcGrains(ebsd('indexed'));

% 2. remove all very small grains
ebsd(grains(grains.grainSize < 5)) = [];

% 3. redo grain reconstruction
[grains,ebsd.grainId] = calcGrains(ebsd('indexed'));

% 4. plot the grain boundaries
plot(grains.boundary,'lineWidth',1.5,'micronbar','off')

% 5. select only very large grains
big_grains = grains(grains.grainSize > 150);

% 6.  plot the crystals
hold on
plot(big_grains('olivine'),0.8*cS,'linewidth',2,'colored')
hold off
legend off

The idea of inverse pole figure color coding of orientation maps is to visualize the orientation of a grain by the color of the crystal face pointing towards you. In the case Olivine habitus this would lead to six different colors. We can overcome this restriction by replacing the colored crystal shape by a colored ball.

close all
ipfKey = ipfHSVKey(ebsd('olivine'));
plot(ipfKey,'3d')

Next we proceed as with the crystal habitus and place a colored ball at each position of the big grains and rotate it according to the meanorientation of the grain.

plot(grains.boundary,'lineWidth',1.5,'micronbar','off')

hold on
plot(big_grains('olivine'),ipfKey)
hold off
legend off

Finally, we take the color in the center of the ball as the color representing the orientation of the grain. This transformation from a list of orientations into a list colors given as RGB values is the central purpose of the color key ipfKey we have defined above and is done by the command ipfKey.orientation2color.

% this computes the colors for each orientation specified as input
colors = ipfKey.orientation2color(big_grains('olivine').meanOrientation);

% this plots the grains colorized according to the RGB values stored in colors
plot(big_grains('o'),colors)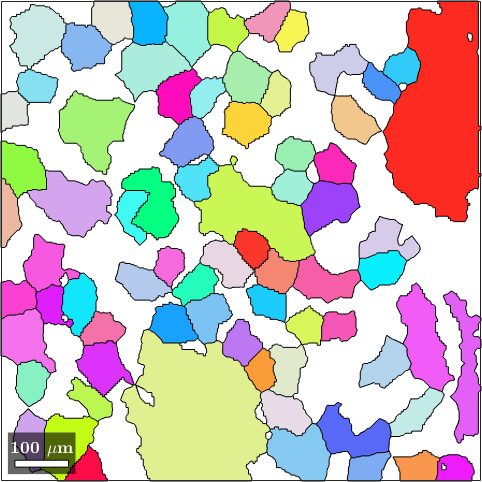

Basic Properties

The interpretation of the colors becomes more simple if we plot the colored ball in stereographic projection and mark the crystallographic axes.

plot(ipfKey,'complete','upper')

h = Miller({1,0,0},{0,1,0},{0,0,1},{1,1,0},{1,0,1},{0,1,1},{1,2,0},{0,2,1},...
  ebsd('olivine').CS);
annotate(h.symmetrise,'labeled','backgroundColor','w')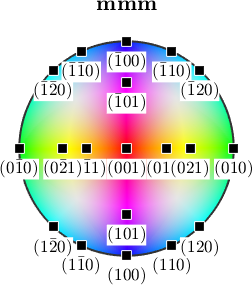

From the colors of the grains in the map we may now deduce for each grain which crystal axis is pointing out of the plane of the specimen. Accordingly, we can associate to each grain a specific point in the color key. Let plot a colored dot for each grain orientation in the inverse pole figure that scales according to the grain area.

plotIPDF(big_grains('olivine').meanOrientation,colors,vector3d.Z,...
  'MarkerSize',0.05*big_grains('olivine').area,'markerEdgeColor','k')

Current plot held
Current plot released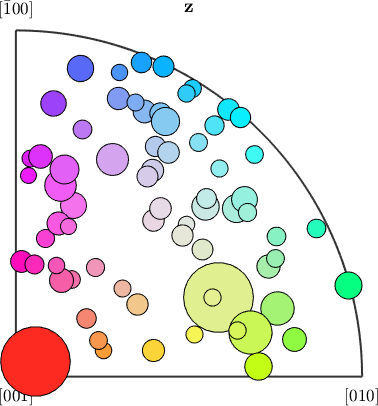

Instead of colorizing which crystal axis is pointing out of the specimen surface we may also colorizing which crystal axis is pointing towards the rolling or folliation direction or any other specimen fixed direction. This reference direction is stored as the property inversePoleFigureDirection in the color key.

% set the reference direction to X
ipfKey.inversePoleFigureDirection = vector3d.X;

% compute the colors
colors = ipfKey.orientation2color(ebsd('olivine').orientations);

% plot the ebsd data together with the colors
plot(ebsd('o'),colors)

Note, that ipfKey.inversePoleFigureDirection may even be a vector of directions. Which is helpful for round specimen where one wants to consider the direction normal to the surface.

Customizing the Color Key

Orientation color keys usually provide several options to alter the alignment of colors. Let's give some examples

% we may interchange green and blue by setting
ipfKey.colorPostRotation = reflection(yvector);

plot(ipfKey)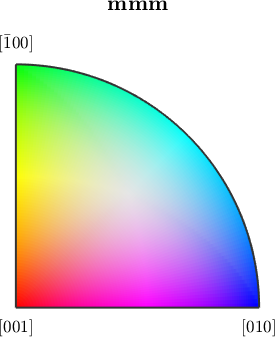

or cycle of colors red, green, blue by

ipfKey.colorPostRotation = rotation.byAxisAngle(zvector,120*degree);

plot(ipfKey)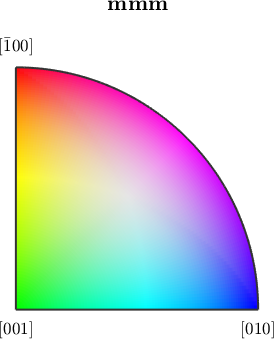

Laue or Enantiomorphic symmetry groups

As the Euler angles provided by the EBSD measurement devices describe proper rotations only they do not include any improper symmetry operation. For this reason it is entirely justified to consider for the ipf map proper symmetries only. Lets define the corresponding color key

% the color key corresponding to the purely enantiomorphic symmetry group
ipfKey = ipfHSVKey(ebsd('olivine').CS.properGroup);
plot(ipfKey)

We obverse that the key is twice as large and hence allows for a better distinction between different orientations.

close all
color = ipfKey.orientation2color(ebsd('olivine').orientations);
plot(ebsd('olivine'),color)

Other inverse pole figure keys

Beside the default ipf color key MTEX provides the default color keys are they are used by other popular EBSD systems.

plot(ipfTSLKey(ebsd('olivine').CS))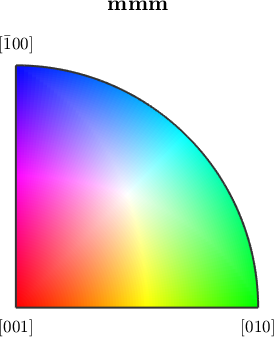

plot(ipfHKLKey(ebsd('olivine').CS))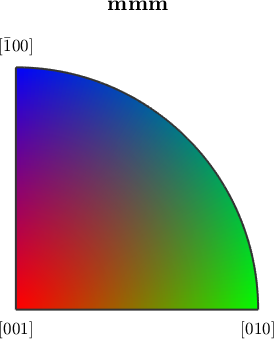

The user should be aware that for certain symmetry groups these color keys lead to color jumps.