doHClustering edit page

hierarchical clustering of rotations and vectors

Syntax

[c,center] = doHCluster(ori,'numCluster',n)
[c,center] = doHCluster(ori,'maxAngle',omega)

Input

ori orientation
n number of clusters
omega maximum angle

Output

c list of clusters
center center of the clusters

Example

% generate orientation clustered around 5 centers
cs = crystalSymmetry('m-3m');
center = orientation.rand(5,cs);
odf = unimodalODF(center,'halfwidth',5*degree)
ori = odf.discreteSample(3000);
odf = SO3FunRBF (m-3m → xyz)
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 5°
  center: 5 orientations
 
  Bunge Euler angles in degree
     phi1     Phi    phi2  weight
  276.984 29.0736 339.765     0.2
  170.784 123.556 345.603     0.2
  348.335 118.777 356.899     0.2
  29.8708 126.781 245.864     0.2
  314.534 64.0075 215.792     0.2
% find the clusters and its centers
tic; [c,centerRec] = calcCluster(ori,'method','hierarchical','numCluster',5); toc
Elapsed time is 2.934888 seconds.
% visualize result
oR = fundamentalRegion(cs)
plot(oR)
oR = orientationRegion
 
 crystal symmetry:  432
 max angle: 62.7994°
 face normales: 14
 vertices: 24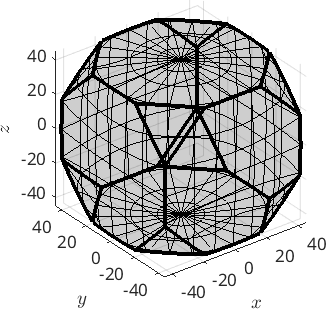
hold on
plot(ori,ind2color(c))
caxis([1,5])
plot(center,'MarkerSize',10,'MarkerFaceColor','k','MarkerEdgeColor','k')
plot(centerRec,'MarkerSize',10,'MarkerFaceColor','r','MarkerEdgeColor','k')
hold off
plot 2000 random orientations out of 3000 given orientations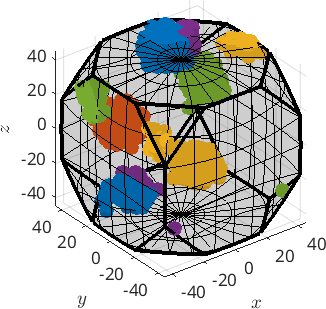
%check the accuracy of the recomputed centers
min(angle_outer(center,centerRec)./degree)
ans =
    7.3142    0.1721    0.2428    0.3278    6.5350