rotates an odf with specimen symmetry into its symmetry axes
centerSpecimen(odf,center) tries to find the normal vectors of orthorhombic symmetry for the x mirror and y mirror plane and calculates an rotation needed to rotate the odf back into these mirror planes. the routine starts with a look around grid for a given center (default xvector) to find a starting value for newton iteration.
Syntax
[odf,rot,v1,v2] = centerSpecimen(odf,v0,varargin)Input
| odf | SO3Fun |
| v0 | vector3d initial guess for a symmetry axis (default xvector) |
Output
| odf | rotated SO3Fun |
| rot | rotation such that rotate(odf_out,r) = odf_in |
| v1,v2 | normal vector of the two fold symmetry axes |
Options
| SO3Grid | a SO3Grid where the SO3Fun is evaluated on |
| delta | specifies the opening angle for the initial search grid around input center |
| resolution | specifies the resolution for the initial search grid |
| silent | don't verbose number of initial axes and the newton iteration |
| Fourier | use Fourier coefficients as objective function |
Example
% starting with an synthetic odf with orthorhombic symmetry
CS = crystalSymmetry('cubic');
SS = specimenSymmetry('orthorhombic');
ori = [orientation.byEuler(135*degree,45*degree,120*degree,CS,SS) ...
orientation.byEuler( 60*degree, 54.73*degree, 45*degree,CS,SS) ...
orientation.byEuler(70*degree,90*degree,45*degree,CS,SS)...
orientation.byEuler(0*degree,0*degree,0*degree,CS,SS)];odf = unimodalODF(SS*ori);% we define a rotational displacement
r2 = rotation.byEuler( 6*degree,4*degree,0*degree);
odf = rotate(odf,r2);
h = [Miller(0,0,1,CS),Miller(0,1,1,CS),Miller(1,1,1,CS)];
plotPDF(odf,h,'antipodal','complete','upper');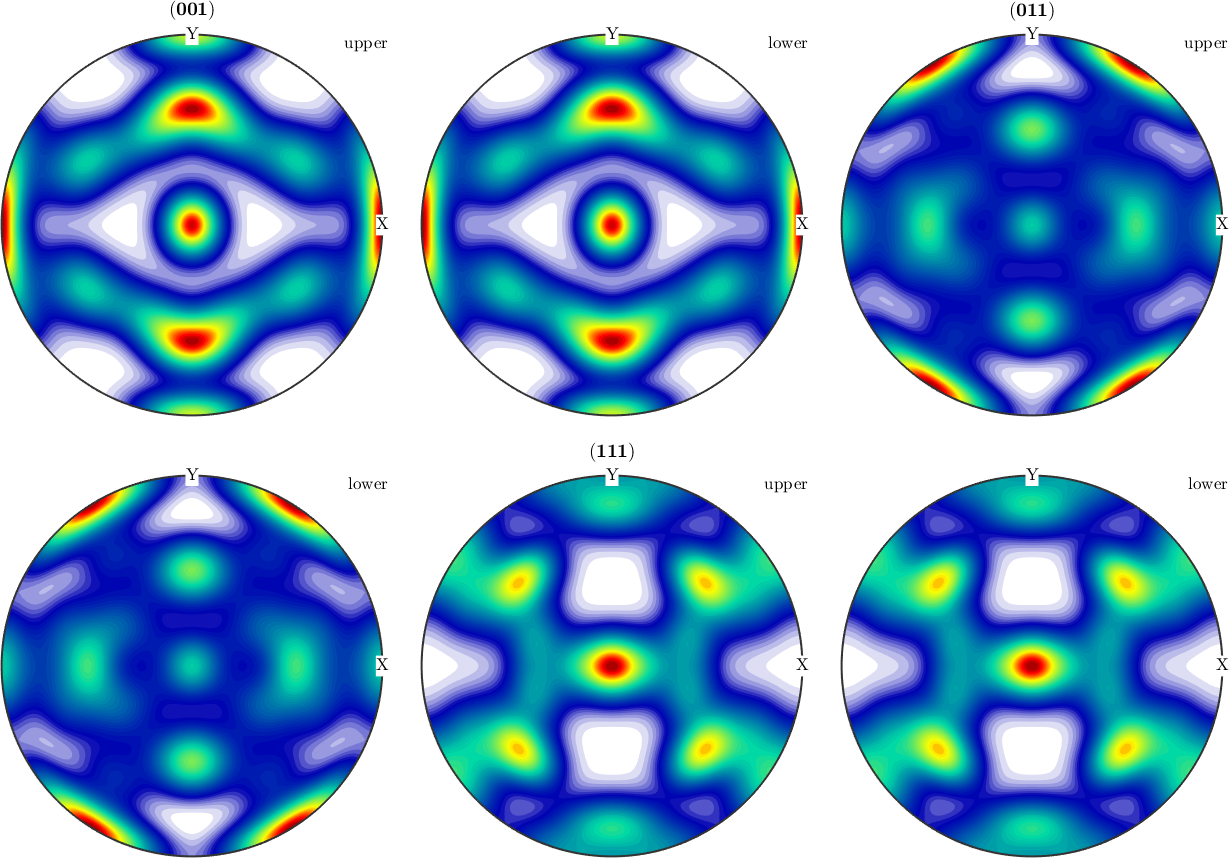
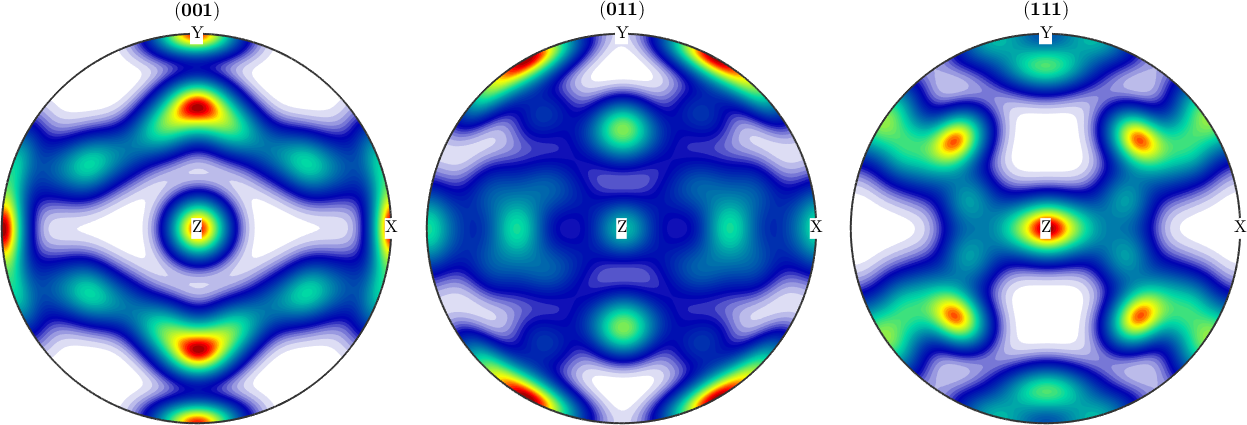
% lets try to retrieve the original orthorhombic odf back
[odr,r,v1,v2] = centerSpecimen(odf);
plotPDF(odr,h,'antipodal')