MTEX Changelog
MTEX 5.2.0 9/2019
Speed Improvements
- much faster visualization of the large EBSD maps if gridify is used
- faster Fourier transforms on the sphere and the orientation space
- support for https://docs.mosek.com/9.0/toolbox/install-interface.html as faster replacement for linprog from the Optimization Toolbox
Support for hexagonal EBSD grids
The function gridify now works also for EBSD data measured on a hexagonal grid. As a consequence denoising and GND computation for those data is also on the way.
Plastic Deformations
MTEX 5.2. introduces a bunch of new tensor classes to make modelling of plastic deformations more straight forward.
The relationships between those tensors are explained in the section plastic deformations.
Spherical Bingham Distribution
Nativ support for spherical Bingham distributions, including the abbility to fit them to directional distributions.
Tensor Visualisation
Improved methods for the vizualisation of ellastic properties, see Seismic demo
Improved Figure Layout
- fix layout
- plot at fixed positions
Misc Changes
- compute the volume of a crystal shape
- label crystal faces in crystal shapes
- new function orientation_std.html for computing the standard deviation of orientations
- calcKearnsFactor
- allow to index ebsd data and grains by id using {} brackets
ebsd{id}
grains{id}- new options to scatter
scatter(v,'numbered') % plot vectors with numbers scatter(v,'MarkerFaceColor','none') % plot vectors with colored empty marks
MTEX 5.1.0 04/2018
Dislocation systems
Starting with version 5.1 MTEX introduces a class representing dislocation systems. Dislocation systems may be lists of edge or screw dislocations and are either defined by its burgers and line vectors
cs = crystalSymmetry('432') b = Miller(1,1,0,cs,'uvw') l = Miller(1,-1,-2,cs,'uvw') dS = dislocationSystem(b,l)
by a family of slipsystems
sS = slipSystem.fcc(cs) dS = dislocationSystem(sS)
or as the family of predefined dominant dislocation systems by
dS = dislocationSystem.fcc(cs)
More information how to calculate with dislocation systems can be found here.
Geometrically neccesary dislocations
The newly introduced dislocation systems play an important role when computing geometrically neccesary dislocations from EBSD data. The workflow is illustrate the script GND_demo and consists of the following steps:
- define the dominant dislocation systems
- transform the dislocation systems into specimen coordinates for each pixel of the EBSD map
- compute the curvature tensor for each pixel in the EBSD map
- fit the dislocation systems to the curvature tensors.
- compute the total energy in each pixel
Tensor arithmetics
dyad, trace, det, mean, diag, eye, sym
Birefringence
MTEX 5.1 includes some basic methods to analyze and simulate optically isotropic materials. This includes the computation of the optical axis, birefringence and spectral transmission. The new features are demonstrated in BirefringenceDemo.
Color Keys
In MTEX 5.1 the color keys used for coloring EBSD have been a bit reorganised.
- seperate classes for directional color keys. So far these classes are HSVDirectionKey, HKLDirectionKey, TSLDirectionKey. This has become neccesary as some orientation color keys depend directional color keys with different symmetry.
- new color key axisAngleColorKey that implements the coloring described in K. Thomsen, K. Mehnert, P. W. Trimby and A. Gholinia: Quaternion-based disorientation coloring of orientation maps, Ultramicroscopy, 2017. In central idea is to colorise the misorientation axis with respect to the specimen reference system.
- The existing color keys have been renamed for better consistency. The new names are BungeColorKey, ipfHSVKey, ipfHKLKey,
, ipfSpotKey, spotColorKey, PatalaColorKey
Spherical functions
- new function discreteSample to compute random samples from spherical density functions
- new option to symmetrise to symmetrise a spherical function with respect to an axis
Misc
- new fuction fitEllipse to assign ellipses to grains
- the functions tensor/symmetrise and S2Fun/symmetrise do support symmetrisation with respect to a certain axis.
- the function export allows to export arbitrary additional properties together with the Euler angles, e.g. the half axes and orientation of the grain ellipses
- the function loadOrientation_generic allows to import arbitrary additional properties together with the orientations, e.g., weights
- new option logarithmic
- new function ODF/gradient to compute the gradient of and ODF at a certain orientation
- explicitely set the number of rows and columns in a MTEXFigure plot with
- EBSD hdf5 interface works now for Bruker data as well
MTEX 5.0.0 03/2018
Replace all executables by two mex files
In MTEX many functionalities are based on the non equispaced fast Fourier transform (NFFT). Until now this dependency was kept under the hood, or more precisely, hidden in external executable files which often caused troubles on MAC systems. Starting with MTEX 5.0. all the executables have been replaced by two mex files provided by the NFFT package. This change (hopefully) comes with the following advantages
- better compatibility with MAC systems, no SIP disabled required
- increased performance, e.g., due to multi core support
- better maintainability, as all MTEX code is now Matlab code
- the pole figure to ODF inversion algorithm is now entirely implemented in Matlab making it simple to tweak it or add more sophisticated inversion algorithms
Spherical functions
Many functions in MTEX compute directional dependent properties, e.g. pole figures, inverse pole figures, wave velocities, density distribution of misorientation axis or boundary normals. Until now those functions took as an input an of vector of directions and gave as an output a corresponding vector of function values, e.g. the command
pfi = calcPDF(odf,Miller(1,0,0,odf.CS),r)
returns for a list of specimen directions r the corresponding list of pole figure intensities pfi for the ODF odf. Starting with MTEX 5.0 it is possible to ommit the list of specimen directions r or replace it by an empty list []. In this case the command
pdf = calcPDF(odf,Miller(1,0,0,odf.CS))
returns a spherical function pdf also called pole density function. One can evaluate this spherical function using the command eval at the list of specimen directions r to obtain the pole figure intensities
pfi = pdf.eval(r)
However, there are many more operations that can be performed on spherical functions:
% compute with spherical functions as with ordinary numbers pdf3 = 5 * pdf1 + 3 * pdf2 pdf = max(pdf,0) % repace of negative entries by 0 pdf = abs(pdf) % take the absolute value sum(pdf) % the integral of the pole figure sum(pdf.^2) % the integral of the pole figure squares - also called pole figure index
% plotting plot(pdf) plot3(pdf) % plot in 3d
% detect maximum value
[value,pos] = max(pdf)% compute the eigen values and eigen vectors
[e,v] = eig(pdf)For a complete list of functions read here.
Symmetry aware spherical functions
Since most of the directional dependent properties obey additional symmetry properties the class S2FunHarmonic has been extended to symmetry in the S2FunHarmonicSym class.
Multivariate spherical functions, vector fields and spherical axis fields
In some cases it is useful that a spherical function gives not only one value for a certain direction but several values. This is equivalent to have concatenate several univariate spherical function to one multivariate function. This can be accomplished by
S2Fmulti = [S2F1,S2F2,S2F3]
which gives a spherical function with 3 values per direction. More information how to work multivariate functions can be found here.
If we interpret the 3 values of S2Fmulti as  ,
, 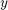 , and,
, and,  coordinate of a 3 dimensional vector, the function S2Fmulti can essentially be seen as a spherical vector field associating to each direction a three dimensional vector. The most important
example of such a vector field is the gradient of a spherical function:
coordinate of a 3 dimensional vector, the function S2Fmulti can essentially be seen as a spherical vector field associating to each direction a three dimensional vector. The most important
example of such a vector field is the gradient of a spherical function:
g = S2F1.grad
The resulting variable g is of type S2VectorField. A complete list of functions available for vector fields can be found here.
Another example for vector fields are polarisation directions pp, ps1, ps2 as computed by
[vp,vs1,vs2,pp,ps1,ps2] = velocity(C)
The main difference is, that polarisation directions are antipodal, i.e. one can not distinguish between the polarisation direction d and -d. In MTEX we call vector fields with antipodal values are represented by variables of type AxisField.
Scalar tensor properties are returned as spherical functions
Any scalar or vectorial property of a tensor is not returned as a spherical function or spherical vector field. Examples are the velocity properties mentioned above, Youngs modulus, shear modulus, Poisson ration etc. In particular, plotting those directional dependend quantities is as simple as
plot(C.YoungsModulus)
This makes the old syntax
plot(C,'plotType','YoungsModulus')
obsolete. It is not supported anymore.
Crystal shapes
MTEX 5.0 introduces a new class crystalShape. This class allows to plot 3-dimensional representations of crystals on top of EBSD maps, pole figures and ODF sections. The syntax is as follows
% define the crystal symmetry cs = loadCIF('quartz');
% define the faces of the crystal m = Miller({1,0,-1,0},cs); % hexagonal prism r = Miller({1,0,-1,1},cs); % positive rhomboedron, usally bigger then z z = Miller({0,1,-1,1},cs); % negative rhomboedron s2 = Miller({1,1,-2,1},cs); % right tridiagonal bipyramid x2 = Miller({5,1,-6,1},cs); % right positive Trapezohedron N = [m,r,z,s2,x2];
% define the crystal shape habitus = 1.2; % determines the overal shape extension = [1,1.2,1]; % determines the extension of the crystal in x,y,z direction cS = crystalShape(N,habitus,extension);
plot(cS) plot(x,y,cS) plot(grains,cS) plot(ebsd,cS) plotPDF(ori,ori*cS)
ODF component analysis
MTEX 5.0 allows for decomposing ODF into components using the command calcComponents. In its simplest form
[mods,weights] = calcComponents(odf)
returns a list of modal orientaions mods and a list of weights which sum up to one. A more advanced call is
[modes, weights,centerId] = calcComponents(odf,'seed',oriList)which returns in centerId also for each orientation from oriList to which component it belongs.
Clustering of orientations
The ODF component analysis is used as the new default algorithm in calcCluster for orientations. The idea is to compute an ODF out of the orientations and call calcComponents with
[center,~,centerId] = calcComponents(odf,'seed',ori)Then center are the clusters center and centerId gives for each orientation to which cluster it belongs. Substantional in this method is the choise of the kernel halfwidth used for ODF computation. This can be adjusted by
[c,center] = calcCluster(ori,'halfwidth',2.5*degree)New tensor classes
With MTEX 5.0 we start introducing specific tensor classes. So far we included the following classes
more tensors are supposed to be included in the future. The central advantage is that tensor specific behaviour and functions can now better be implemented and documented, e.g., that the inverse of the compliance tensor is the stiffness tensor and vice versa. For user the important change is that e.g. the stiffness tensor is now defined by
C = stiffnessTensor(M,cs)
instead of the depreciated syntax
C = tensor(M,cs,'name','ellastic stiffness','unit','GPA')
Improved spherical plotting
In MTEX 4.X it was not possible to display the upper and lower hemisphere in pole figure plots, inverse pole figure plots or ODF section plots. This was a server restriction as for certain symmetries both hemispheres do not have to coincide. In MTEX 5.0 this restriction has been overcome. MTEX automatically detects whether the upper and lower hemisphere are symmetrically equivalent and decides whether both hemispheres needs to be plotted. As in the previous version of MTEX this can be controlled by the options upper, lower and complete.
As a consequence the behaviour of MTEX figures have changed slightly. By default MTEX now always plots into the last axis. In order to annotate orintations or directions to all axes in a figure use the new option add2all.
plotIPDF(SantaFe,[xvector,yvector+zvector]) [~,ori] = max(SantaFe) plot(ori,'add2all')
We also introduced two new functions plotSection and quiverSection to visualize spherical functions restricted to a plane. As an exaple one can now plot the slowness surfaceses of wave velocities in the plane perpendicular to Y with
plotSection(1./vp,vector3d.Y)
see here for more information.
Other new functions
- odf.grad computes the gradient of an ODF at some orientation
- grain2d.hist can now plot histogram of arbitrary properties
- ODF.fibreVolume works also for specimen symmetry
- allow to change the length of the scaleBar in EBSD plots
MTEX 4.5.2 11/2017
This is mainly a bug fix release
- some more functions get tab completetion for input arguments
- the option 'MarkerSize' can also be a vector to allow for varying Markersize
- new option 'noSymmetry' for plotPDF and plotSection
orientation relation ships
- new functions for computing variants and parents for a orientation relation ship *
- new predefined orientation relation ship
gT = GreningerTrojano(csAlpha,csGamma) ori_childs = ori_parent * inv(gT.variants) ori_parents = ori_child * gT.parents
MTEX 4.5.1 08/2017
This is mainly a bug fix release
- some functions get tab completetion for input arguments
- allow different colormaps in one figure
- updated interfaces
- added Levi Civita permutation tensor
- improved round2Miller
- grains.boundary('phase2','phase1') rearranges the misorientation to be from phase2 to phase 1
MTEX 4.5 03/2017
3d orientation plots
MTEX 4.5 supports plotting of orientations, fibres, and ODFs in 3d in various projections like
- Bunge Euler angles
- Rodrigues Frank space
- axis angles space
Misorientations
- MTEX introduces round2Miller which determines to an arbitrary misorientation mori two pairs of lower order Miller indeces such that which are aligned by mori
- MTEX includes now some of the important misorientation relationsships like
orientation.Bain(cs) orientation.KurdjumovSachs(cs) orientation.NishiyamaWassermann(cs) orientation.Pitch(cs)
Grain Reconstruction
New option to handle non convex other shapes of EBSD data sets
calcGrains(ebsd,'boundary','tight')
- Grain boundary indexing* The commands gB('phase1','phase2').misorientation returns now always a misorientation from phase1 to phase2
Tensors
EBSD
Rotating, flipping of EBSD data is now done with respect to the center of the map. Previously all these opertions where done relatively to the point (0,0). Use
rotate(ebsd,180*degree,'center',[0,0])to get back the behavior of previous versions.
Colorbar
MTEXColorbar allows now to have a title next to it. Use
mtexColorbar('Title','this is a title')
Bug Fix This release contains several important bug fixes compare to MTEX 4.4.
MTEX 4.4 01/2017
Slip Systems
MTEX 4.4 introduces support for slip systems. Slip systems are defined by a plane normal and a slip direction
sSFCC = slipSystem(Miller(0,1,-1,cs,'uvw'),Miller(1,1,1,cs,'hkl'));
Slip systems are instrumental for computating the following properties
Fibres
MTEX 4.4 adds support for fibres in orientation space. As an example the alpha fibre in cubic materials can be defined in the following ways
- as a predefined fibre
cs = crystalSymmetry('m-3m')
f = fibre.alpha(cs)- by a pair of directions
f = fibre(Miller(1,0,0,cs),vector3d.X)
- by two orientations
ori1 = orientation('Miller',[0 0 1],[1 1 0],cs); ori2 = orientation('Miller',[1 1 1],[1 1 0],cs);
f = fibre(ori1,ori2)
- by a list of orientations
f = fibre.fit([ori1,ori2,mean(ori1,ori2)])
All commands that took a pair of directions to specify a fibre, e.g., fibreODF, fibreVolume, plotFibre have been rewritten to accept a fibre as a single input argument. I.e. a fibre ODF is now defined by
odf = fibreODF(fibre.alpha(cs))
Up to now the following functions are implemented for fibres
- plot to Rodrigues space, Euler space, pole figures, inverse pole figures
oR = fundamentalRegion(cs,cs) f = fibre(oR.V(1),oR.V(2)) plot(oR) hold on plot(fibre,'color','r','linewidth',2) hold off
- compute the angle between orientation and fibre
angle(f,ori)
Ignore Symmetry
Many functions support now the flag noSymmetry. Among them are angle, axis, dot, cunion.
Clustering of orientations
The new command cluster allows to cluster a given set of orientations into a given number of clusters.
% generate orientation clustered around 5 centers cs = crystalSymmetry('m-3m'); center = orientation.rand(5,cs); odf = unimodalODF(center,'halfwidth',5*degree) ori = odf.calcOrientations(3000);
% find the clusters and its centers [c,centerRec] = cluster(ori,'numCluster',5);
% visualize result
oR = fundamentalRegion(cs);
plot(oR)hold on plot(ori.project2FundamentalRegion,c) caxis([1,5]) plot(center.project2FundamentalRegion,'MarkerSize',10,'MarkerFaceColor','k','MarkerEdgeColor','k') plot(centerRec.project2FundamentalRegion,'MarkerSize',10,'MarkerFaceColor','r','MarkerEdgeColor','k') hold off
MTEX 4.3.2 07/2016
Alignment of Miller plots
You can now specify the alignment of the crystal a-axis or b-axis in Miller plots by
plota2north, plota2east, plota2south, plota2west plotb2north, plotb2east, plotb2south, plotb2west
This might also be specify in mtex_settings.m mtex_settings.
MTEX 4.3 - 03/2016
Alignment of Miller plots
Starting with MTEX 4.3 plots with respect to the crystal coordinate system, i.e., inverse pole figure plots, misorientation axis plot, ipf keys, are always aligned such that the b-axis points towards east. This follows the convention given in the International Table of Crystallography. The alignment can be adjusted using the option xAxisAlignment
plot(Miller(1,0,0,cs),'xAxisAlignment',30*degree)Plotting vector fields at grain centers or grain boundaries
There are three new commands
that allow visualizing directions for EBSD data, grains and at grain boundaries. The input argument dir should be a list of vector3d and may represent e.g. slip directions, polarization direction, etc.
EBSD data in raster format
Until MTEX 4.2 EBSD data have been always considered as a one-dimensional list of data, i.e., the often present structure of a regular grid was completely ignored. Starting with MTEX 4.3 EBSD data can be converted in a regular grid by
ebsd = ebsd.gridify
Missing data are represented as NaN in the regular representation. Gridified EBSD data may be addressed analogously like matrixes, i.e.,
ebsd(100,200)
will give pixel 100 in the y-direction and 200 in the x-direction. Analogously.
ebsd(50:100,:)
will give the stripe if pixels with y coordinate between 50 and 100.
Orientation gradients and GND
Gridified EBSD data allows also to compute orientation gradients by
ebsd.gradientX ebsd.gradientY
as well as an estimate of the geometrically necessary dislocation density (GND) using the command calcGND
ebsd.calcGND
Auxilary new functionality
- grain2d.calcParis - Percentile Average Relative Indented Surface
- tensor.diag
- reduce works now also for EBSD data on Hex grids
MTEX 4.2 - 11/2015
MTEX 4.2 introduces basic functionality for triple junction analysis in grain maps.
Triple points
Triple points are automatically computed during grain reconstruction and can be accessed by
grains.triplePoints grains.boundary.triplePoints
More details on how to work with triple points can be found here.
large EBSD data sets
Analyzing large EBSD data sets may be quite annoying due to memory consumption and slow plotting. As a work around MTEX includes a new function reduce which allows reducing the data set to each n-th pixel, i.e.,
ebsd_small = reduce(ebsd,2)
contains only 25 percent of the data of the original data set. This functionality is assumed to be used for experimenting around with the data set and setting up a proper analysis script. The final analysis should, if possible, be done with the entire data set.
New option to ignore symmetry
When computing the angle between crystal directions, the misorientation angle between orientations and the misorientation axis symmetry can be ignored with the flag noSymmetry
angle(Miller(1,0,0,cs),Miller(0,1,0,cs),'noSymmetry') angle(mori,'noSymmetry') axis(mori,'noSymmetry')
Axis distributions in specimen coordinates
In order to plot axis distributions in specimen coordinates, you can now do
[ori1,ori2] = calcMisorientation(ebsd('phaseName')) plotAxisDistribution(ori1,ori2,'contourf')
or
ori = ebsd(grains.boundary('indexed').ebsdId).orientations plotAxisDistribution(ori(:,1),ori(:,2),'contourf')
New option to work around Matlab opengl bug
In mtex_settings.m mtex_settings there is a new option that may help to work around the Matlab opengl bug. Switching it of may give nicer graphics.
setMTEXpref('openglBug',true)CSL misorientations
The function CSL requires now as a mandatory argument the crystal symmetry of the phase, i.e.
CSL(3,crystalSymmetry('m-3m'))Grain boundaries
Grain boundaries segments have a new option midPoint which may be used for attaching a vector displaying the misorientation axis or some other direction.
More ODF sections
- phi1
- Phi
- gamma
- omega
Along with the old syntax, there is now a new syntax that allows for more fine control of the ODF sections.
oS = phi2Sections(odf.CS,odf.SS) oS.phi2 = [ 10*degree, 30*degree, 90*degree ];
plot(odf,oS)
Ordering of crystal symmetries
One can now check whether a crystal symmetry cs1 is a subgroup of crystal symmetry cs2 by
cs1 <= cs2
Further, the largest proper subgroup of some crystal symmetry cs is now accessible by
cs.properSubGroup
MTEX 4.1 - 09/2015
MTEX 4.1 introduces new possibilities to the analysis of misorientations. For the first time, it covers all geometric aspects of misorientations between arbitrary crystal symmetries. Furthermore, MTEX 4.1 introduces filters to smooth EBSD data.
Smoothing of EBSD Data
Smoothing of EBSD data might be necessary if the orientation data are corrupted by noise which influences the estimation of orientation dependent properties like KAM or GND. The general syntax for smoothing EBSD data is
ebsd = smooth(ebsd)
This applies the spline filter to the orientation data. Beside the spline filter, many other filters are available. A general discussion on this topic can be found here. To make use of a different than the dafault filter use the syntax
F = medianFilter
F.numNeighbours = 2 % this way options for the filter can be set
ebsd = smooth(ebsd,F)The command smooth can also be used to fill not indexed measurement points. This behavior is enabled by the option fill
ebsd = smooth(ebsd,F,'fill')Support for antipodal symmetry for misorientations
When working with boundary misorientations between the same phase one can not distinguish between a misorientation mori and its inverse |inv(mori). Starting with MTEX 4.1 this symmetry is supported for misorientations and misorientation distribution functions.
mori = inv(ori1) * ori2; mori.antipodal = true;
mdf = calcMDF(odf1,odf2,'antipodal')Antipodal symmetry effects the asymmetric region in orientation space as described below, as well as the distance between misorientations. Boundary misorientations between the same phase have set the flag antipodal by default.
Asymmetric regions in orientation space
MTEX 4.1 has now full support of asymmetric regions in orientation space. For any combination of crystal symmetries they can be defined by
oR = fundamentalRegion(cs1,cs2)
and visualized by
plot(oR)
One can check, whether an orientation is within the fundamental region by
oR.checkInside(ori)
similarly as for a sphericalRegion. The fundamental region with antipodal symmetry is defined by.
oR = fundamentalRegion(cs1,cs2,'antipodal')For a fixed rotational angle omega, the intersection of the fundamental region with the sphere with radius omega gives the fundamental sector for the corresponding rotational axes. The axis sector can be computed by
sR = oR.axisSector(omega)
Axis and angle distributions
Thanks to the implementation of the asymmetric region plotAxisDistribution and plotAngleDistribution works in MTEX 4.1 for any combination of crystal symmetries.
The following syntax is obsolete
plotAxisDistribution(grains.boundary('phase1','phase2')) plotAngleDistribution(grains.boundary('phase1','phase2')) plotAngleDistribution(ebsd)
As replacement use the more verbose syntax
plotAxisDistribution(grains.boundary('phase1','phase2').misorientation) plotAngleDistribution(grains.boundary('phase1','phase2').misorientation)
mori = calcMisorientation(ebsd('phase1'),ebsd('phase2')) plotAngleDistribution(mori) plotAxisDistribution(mori)
Rotational axis in specimen coordinates
It is now possible to compute the misorientation axis between two orientations in specimen coordinate system. This is done by
axis(ori1,ori2)
To do so with random misorientations from an EBSD data set do
[ori1,ori2] = calcMisorientation(ebsd('phase1'),ebsd('phase2')) plot(axis(ori1,ori2))
Axis angle plots
(Mis)Orientation, ODFs, and MDFs can now be plotted in axis angles sections. Those plots respect the fundamental sector depending on the misorientation angle and for all combinations of crystal symmetries. The angle sections are scaled such that they represent the corresponding volume in orientation space. This can be switch off as described below
plotSection(mori,'axisAngle',55*degree) plotSection(mdf,'axisAngle',(15:10:55)*degree) plotSection(mdf,'axisAngle',(15:10:55)*degree,'volumeScaling',false) plotSection(mdf,'axisAngle',(15:10:55)*degree,'antipodal')
Replace plotODF by a plotSection
In most cases, you can replace plotODF by a|plot|. Only for misorientations, the default plot is scattered.
More default settings for EBSD maps and pole figure plots
- new MTEXpref to show/hide the micronbar in EBSD maps. The default is set in mtex_settings.m to on. The following command switches them off.
setMTEXpref('showMicronBar','off')
- new MTEXpref to show/hide the coordinates in EBSD maps. The default is set in mtex_settings.m to off. The following command switches them on.
setMTEXpref('showCoordinates','off')
- new MTEXpref to display coordinates in pole figure plot. The default is set in mtex_settings.m to display the directions X and Y. The following command switches it to RD and ND.
pfAnnotations = @(varargin) text([vector3d.X,vector3d.Y],{'RD','ND'},...
'BackgroundColor','w','tag','axesLabels',varargin{:});
setMTEXpref('pfAnnotations',pfAnnotations);Other improvements since MTEX 4.0.0
During the minor revisions of MTEX also several minor improvements have been added which are summarized below
- check for inclusions in grains: the following command returns a list of true/false depending whether a grain in grainList is an inclusion in hostGrain
hostGrain.checkInside(grainList)
- allow syntax
plot(odf,pf.h,'superposition',pf.c)- allow to show / hide the scale bar by the MTEX menu or by
[~,mP] = plot(ebsd)
mP.micronBar.visible = 'off'- allow to place labels above/below the marker by
plot(xvector,'label','RD','textAboveMarker')
- new EBSD interface to ACOM Nanomegas *.ang files
- plot relative to the crystal coordinate system are now always aligned such that x points to the east and y points to north
- misorientation axis with respect to crystal and specimen reference frame
a = axis(o1,o2) % misorientation axis with respect to sample coordinate systema = axis(inv(o2)*o1) % misorientation axis with respect to crystal coordinate system- new function intersect to compute intersections between grain boundary segments an a line
[x,y] = grains.boundary.intersect(xy1,xy2);
- option for plotting angle distributions in percent
plotAngleDsitribution(mori,'percent')- reintroduced min/max in pole figure like plot
plot(pf,'minmax')- 3d plots of pole figures can now be simultanously rotated
- you can now restrict an EBSD data set to a line to plot profiles
ebsd_prof = ebsd.spatialProfile(ebsd,some_line)
- additional syntax to define a list if Miller indices
h = Miller({1,0,0},{1,1,1},{2,3,4},CS,'uvw')- interface to Bruker phl files
- new properties for grainBoundary gB
gB.segmentLength % length of the corresponding connected segment gB.isTwinning(mori,threshold) % check boundary for twinning
- for a crystal symmetry cs you can access a, b ,c and reciprocal axes by
cs.Aaxis cs.AaxisRec
- compute KAM with misorientation angle threshold or grain boundary threshold
MTEX 4.0.0 - 10/2014
MTEX 4 is a complete rewrite of the internal class system which was required to keep MTEX compatible with upcoming Matlab releases. Note that MTEX 3.5 will not work on Matlab versions later than 2014a. As a positive side effect, the syntax has been made more consistent and powerful. On the bad side MTEX 3.5. code will need some adaption to run on MTEX 4. There are two general principles to consider
Use dot indexing instead of getting and setting methods
The syntax
h = get(m,'h') m = set(m,'h',h+1)
is obsolete. set and get methods are not longer supported by any MTEX class. Instead use dot indexing
h = m.h m.h = h + 1
Note, that this syntax can be nested, i.e., one can write
ebsd('Forsterite').orientations.angleto get the rotational angle of all Forsterite orientations, or,
cs.axes(1).x
to get the x coordinate of the first crystallographic coordinate axis - the a-axis. As a nice bonus, you can now use TAB completion to cycle through all possible properties and methods of a class.
Use camelCaseCommands instead of under_score_commands
Formerly, MTEX used different naming conventions for functions. Starting with MTEX 4.0 all function names consisting of several words, have the first word spelled with lowercase letters and the consecutive words starting with a capital letter. Most notable changes are * plotPDF * plotIPDF * plotODF * calcError
Grain boundaries are now directly accessible
MTEX 4.0 introduces a new type of variables called grainBoundary which allows to represent arbitrary grain boundaries and to work with them as with grains. The following lines give some examples. Much more is possible.
% select boundary from specific grains
grains.boundary% select boundary by phase transistion gB = grains.boundary('Forstarite','Enstatite')
% select boundary by misorientation angle
gB(gB.misorientation.angle>100*degree)% compute misorientation angle distribution for specific grain boundaries
plotAngleDistribution(gB)Plotting EBSD, grain, grainBoundary data has different syntax
The syntax of the plot commands has made more consistent throughout MTEX. It is now
plot(obj,data)
where obj is the object to be plotted, i.e., EBSD data, grains, grain boundaries, spherical vectors, pole figures, etc., and the data are either pure numbers or RGB values describing the color. Examples are
% plot MAD values of EBSD data
plot(ebsd,ebsd.mad)% colorize grains according to area
plot(grains,grains.area)% colorize grain boundary according to misorientation angle gB = grains.boundary('Forsterite','Enstatite') plot(gB,gB.misorientation.angle)
Colorization according to phase or phase transition is the new default when calling plot without data argument, i.e., the following results in a phase plot
plot(ebsd)
In order to colorize ebsd data according to orientations, one has first to define an orientationMapping by
oM = ipdfHSVOrientationMapping(ebsd('Forsterite'))Then one can use the command oM.orientation2color to compute RGB values for the orientations
plot(ebsd('Forsterite'),oM.orientation2color(ebsd('Forsterite').orientations))
The orientation mapping can be visualized by
plot(oM)
EBSD data are always spatially indexed
Starting with MTEX 4.0 EBSD data alway have to have x and y coordinates. EBSD data without spatial coordinates are imported simply as orientations. As a consequence, all orientation related functionalities of EBSD data have been moved to orientations, i.e., you can not do anymore
plotpdf(ebsd('Fo'),Miller(1,0,0,CS)) calcODF(ebsd('Fo')) volume((ebsd('Fo'))
But instead you have to explicitely state that you operate on the orientations, i.e.
plotpdf(ebsd('Fo').orientations,Miller(1,0,0,ebsd('Fo').CS)) calcODF(ebsd('Fo').orientations) volume((ebsd('Fo').orientations)
This makes it more easy to apply the same functions to misorientations to grain mean orientations grains.meanOrientation, ebsd misorientation to mean mean |ebsd.mis2mean or boundary misorientations grains.boundary.misorientation
Different syntax for reconstructing grains from EBSD data
In MTEX 3.5 the command
grains = calcGrains(ebsd)
duplicates the ebsd data into the grain variable allowing to access the EBSD data belonging to a specific grain by
get(grains(1),'EBSD')In MTEX 4.0 the command calcGrains returns as an additional output the list of grainIds that is associated with the EBSD data. When storing these grainIds directly inside the EBSD data, i.e., by
[grains,ebsd.grainId] calcGrains(ebsd)
one can access the EBSD data belonging to a specific grain by the command
ebsd(grains(1))
MTEX 4.0 distinguishes between crystal and specimen symmetry
In MTEX 4.0 two new variable types specimenSymmetry and crystalSymmetry have been introduced to distinguish clearly between these two types of symmetry. Calling
cs = symmetry('m-3m') ss = symmetry('triclinic')
is not allowed anymore! Please use instead
cs = crystalSymmetry('m-3m','mineral','phaseName') ss = specimenSymmetry('triclinic')
Pole figure indexing is now analogously to EBSD data
You can now index pole figure data by conditions in the same manner as EBSD data. E.g. the condition
condition = pf.r.theta < 80 * degree
is an index to all pole figure data with a polar angle smaller than 80 degree. To restrict the pole figure variable pf to the data write
pf_restrcited = pf(condition)
In the same manner, we can also remove all negative intensities
condition = pf.intensities < 0 pf(condition) = []
In order to address individuell pole figures within a array of pole figures pf use the syntax
pf('111')or
pf(Miller(1,1,1,cs))
The old syntax
pf(1)
for accessing the first pole figure will not work anymore as it now refers to the first pole figure measurement. The direct replacement for the above command is
pf({1})MTEX 4.0 supports all 32 point groups
In MTEX 4.0 it is for the first time possible to calculate with reflections and inversions. As a consequence, all 32 point groups are supported. This is particularly important when working with piezoelectric tensors and symmetries like 4mm. Moreover, MTEX distinguishes between the point groups 112, 121, 112 up to -3m1 and -31m.
Care should be taken, when using non-Laue groups for pole figure or EBSD data.
Support for three-digit notation for Miller indices of trigonal symmetries
MTEX 4.0 understands now uvw and UVTW notation for trigonal symmetries. The following two commands define the same crystallographic direction, namely the a1-axis
Miller(1,0,0,crystalSymmetry('-3m'),'uvw')
Miller(2,-1,-1,0,crystalSymmetry('-3m'),'UVTW')
Improved graphics
MTEX can now display colorbars next to pole figure, tensor or ODF plots and offers much more powerfull options to customize the plots with titles, legends, etc.
Functionality that has been (temporarily) removed
This can be seen as a todo list.
- 3d EBSD data handling + 3d grains
- some grain functions like aspectRatio, equivalent diameter
- logarithmic scaling of plots
- 3d plot of ODFs
- some of the orientation color maps
- fibreVolume in the presence of specimen symmetry
- Dirichlet kernel
- patala colorcoding for some symmetry groups
- v.x = 0
- misorientation analysis is not yet complete
- some colormaps, e.g. blue2red switched
- histogram of volume fractions of CSL boundaries
- remove id from EBSD?
- changing the phase of a grain should change phases in the boundary
- KAM and GOSS may be improved
- write import wizard for orientations, vectors, tensors.
MTEX 3.5.0 - 12/2013
Misorientation colorcoding
- Patala colormap for misorientations
- publication: S. Patala, J. K. Mason, and C. A. Schuh, Improved representations of misorientation information for grain boundary, science, and engineering, Prog. Mater. Sci., vol. 57, no. 8, pp. 1383-1425, 2012.
- implementation: Oliver Johnson
- syntax:
plotBoundary(grains('Fo'),'property','misorientation','colorcoding','patala')
Fast multiscale clustering (FMC) method for grain reconstruction
- grain reconstruction algorithm for highly deformed materials without sharp grain boundaries
- publication: C. McMahon, B. Soe, A. Loeb, A. Vemulkar, M. Ferry, L. Bassman, Boundary identification in EBSD data with a generalization of fast multiscale clustering, Ultramicroscopy, 2013, 133:16-25.
- implementation: Andrew Loeb
- syntax:
grains = calcGrains(ebsd,'FMC')Misc changes
- one can now access the grain id by
get(grains,'id')- the flags 'north' and 'south' are obsolete and have been replaced by 'upper' and 'lower'
- you can specify the outer boundary for grain reconstruction in nonconvex EBSD data set by the option 'boundary'
poly = [ [x1,y1];[x2,y2];[xn,yn];[x1,y1] ]
grains = calcGrains(ebsd,'boundary',poly)- you can select a polygon interactively with the mouse using the command
poly = selectPolygon
Bug fixes
- .osc, .rw1 interfaces improved
- .ang, .ctf interfaces give a warning if called without one of the options convertSpatial2EulerReferenceFrame or convertEuler2SpatialReferenceFrame
- fixed: entropy should never be imaginary
- removed function SO3Grid/union
- improved MTEX startup
- many other bug fixes
- MTEX-3.5.0 should be compatible with Matlab 2008a
MTEX 3.4.2 - 06/2013
bugfix release
- fixed some inverse pole figure color codings
- option south is working again in pole figure plots
- geometric mean in tensor averagin, thanks to Julian Mecklenburgh
- improved support of osc EBSD format
- tensor symmetry check error can be turned of and has a more detailed error message
- improved syntax for Miller Miller(x,y,z,'xyz',CS) Miller('polar',theta,rho,CS)
- ensure same marker size in EBSD pole figure plots
- allow plotting Schmid factor for grains and EBSD data
- allow to annotate Miller to AxisDistribution plots
- improved figure export
- allow for negative phase indices in EBSD data
- bug fix: https://code.google.com/p/mtex/issues/detail?id=115
- improved ODF fibre plot
MTEX 3.4.1 - 04/2013
bugfix release
- much improved graphics export to png and jpg files
- improved import wizard
- Miller(2,0,0) is now different from Miller(1,0,0)
- new EBSD interfaces h5, Bruker, Dream3d
- various speedups
- fix: startup error http://code.google.com/p/mtex/issues/detail?id=99
- fix: Rigaku csv interface
MTEX 3.4.0 - 03/2013
New plotting engine
MTEX 3.4 features a completely rewritten plotting engine. New features include
- The alignment of the axes in the plot is now described by the options xAxisDirection which can be north, west, south, or east, and zAxisDirection which can be outOfPlane or intoPlane. Accordingly, there are now the commands
plotzOutOfPlane, plotzIntoPlane
- The alignment of the axes can be changed interactively using the new MTEX menu which is located in the menubar of each figure.
- northern and southern hemisphere are now separate axes that can be stacked arbitrarily and are marked as north and south.
- Arbitrary plots can be combined in one figure. The syntax is
ax = subplot(2,2,1) plot(ax,xvector)
- One can now arbitrarily switch between scatter, contour and smooth plots for any data. E.g. instead of a scatter plot the following command generates now a filled contour plot
plotpdf(ebsd,Miller(1,0,0),'contourf')- obsolete options: fliplr, flipud, gray,
Colormap handling
- User defined colormap can now be stored in the folder colormaps, e.g. as red2blueColorMap.m and can set interactively from the MTEX menu or by the command
mtexColorMap red2blueODF
- The default ODF plot is now phi2 sections with plain projection and (0,0) being at the top left corner. This can be changed interactively in the new MTEX menu.
- The computation of more than one maximum is back. Use the command
[modes, values] = calcModes(odf,n)
EBSD data
- MTEX is now aware about the inconsistent coordinate system used in CTF and HKL EBSD files for Euler angles and spatial coordinates. The user can now convert either the spatial coordinates or the Euler angles such that they become consistent. This can be easily done by the import wizard or via the commands
% convert spatial coordinates to Euler angle coordinate system loadEBSD('filename','convertSpatial2EulerReferenceFrame')
% convert Euler angles to spatial coordinate system loadEBSD('filename','convertEuler2SpatialReferenceFrame')
- It is now possible to store a color within the variable describing a certain mineral. This makes phase plots of EBSD data and grains more consistent and customizable.
CS = symmetry('cubic','mineral','Mg','color','red')
- A better rule of thumb for the kernel width when computing an ODF from individual orientations via kernel density estimation.
- inpolygon can be called as
inpolygon(ebsd,[xmin ymin xmax ymax])
Tensors
- new command to compute the Schmid tensor
R = SchmidTensor(m,n)
- new command to compute Schmid factor and active slip system
[tauMax,mActive,nActive,tau,ind] = calcShearStress(stressTensor,m,n,'symmetrise')- it is now possible to define a tensor only by its relevant entries. Missing entries are filled such that the symmetry properties are satisfied.
- faster, more stable tensor implementation
- new syntax in tensor indexing to be compatible with other MTEX classes. For a 4 rank thensor C, we have now
% extract entry 1,1,1,1 in tensor notation
C{1,1,1,1}% extract entry 1,1 in Voigt notation
C{1,1}- For a list of tensors C we have
% extract the first tensor
C(1)Import / Export
- command to export orientations
export(ori,'fname')- command to import vector3d
v = loadVector3d('fname','ColumnNames',{'x','y','z'}) v = loadVector3d('fname','ColumnNames',{'latitude','longitude'})
- new interface for DRex
- new interface for Rigaku
- new interface for Saclay
General
- improved instalation / uninstalation
- new setting system
setpref('mtex','propertyName','propertyValue')
has been replaced by
setMTEXpref('propertyName','propertyValue')
MTEX 3.3.2 - 01/2013
bugfix release
- fix: better startup when using different MTEX versions
- fix: backport of the tensor fixes from MTEX 3.4
- fix: show normal colorbar in ebsd plot if scalar property is plotted
- fix: http://code.google.com/p/mtex/issues/detail?id=82
- fix: http://code.google.com/p/mtex/issues/detail?id=76
- fix: http://code.google.com/p/mtex/issues/detail?id=48
- fix: http://code.google.com/p/mtex/issues/detail?id=71
- fix: http://code.google.com/p/mtex/issues/detail?id=70
- fix: http://code.google.com/p/mtex/issues/detail?id=69
- fix: http://code.google.com/p/mtex/issues/detail?id=65
- fix: http://code.google.com/p/mtex/issues/detail?id=68
MTEX 3.3.1 - 07/2012
bugfix release
- fix: single/double convention get sometimes wrong with tensors
- fix: tensor checks did not respect rounding errors
- fix: ingorePhase default is now none
- fix: calcAngleDistribution works with ODF option
- fix: respect rounding errors when importing pole figures and ODFs
MTEX 3.3.0 - 06/2012
Grains: change of internal representation
Reimplementation of the whole grain part:
get(grains,'EBSD')- the grain selector tool for spatial grain plots was removed, nevertheless, grains still can be selected spatially.
- scripts using the old grain engine may not work properly, for more details of the functionalities and functioning of the @GrainSet please see the documentation.
- new functionalities: merge grains with certain boundary.
EBSD
The behavior of the 'ignorePhase' changed. Now it is called in general 'not indexed' and the not indexed data is imported generally. If the crystal symmetry of an EBSD phase is set to a string value, it will be treated as not indexed. e.g. mark the first phase as 'not indexed'
CS = {'not indexed',...
symmetry('cubic','mineral','Fe'),...
symmetry('cubic','mineral','Mg')};By default, calcGrains does also use the 'not Indexed' phase.
- create customized orientation colormaps
Other
- the comand set_mtex_option is obsolete. Use the matlab command setMTEXpref(...) instead. Additionally, one can now see all options by the command getpref('mtex')
MTEX 3.2.3 - 03/2012
bugfix release
- allow zooming for multiplot objects again; change the z-order of axes
- symmetries allows now options a | | x additional to x | | a
- fix http://code.google.com/p/mtex/issues/detail?id=35
- fix http://code.google.com/p/mtex/issues/detail?id=38
- fix http://code.google.com/p/mtex/issues/detail?id=28
- fix export odf
MTEX 3.2.1 - 11/2011
New Features
- Import and Export to VPSC
- export EBSD data with all properties
- improved ODF calculation from pole figures by using quadrature weights for the pole figure grid
- implemented spherical Voronoi decomposition and computation of spherical quadrature weights
- plot odf-space in omega-sections, the i.e. generalization of sigma-sections
Bug Fixes
- S2Grid behaves more like vector3d
- vector3d/eq takes antipodal symmetry into account
- Euler angle conversion was sometimes wrong
- tensors multiplication was sometimes wrong
- rank 3 tensors get options 'doubleConvention' and 'singleConvention' for the conversion into the Voigt matrix representation
- documentation fixes
- Miller('[100]') gives not the correct result
- import wizard now generates correct CS definition
- import filter for uxd files should now work more reliable
MTEX 3.2 - 05/2011
3d EBSD Analysis
This release for the first time supports 3d EBSD data. In particular, MTEX is now able to
- import 3d EBSD data from stacked files
- visualize 3d EBSD data by plotting interactive slices through the specimen
- 3d grain detection
- the topology of 3d grains, i.e. boundaries, neighboring grains, etc.
Misorientation Analysis
- computation of the uncorrelated misorientation distribution (MDF) for one or two ODFs
- computation of the theoretical angle distribution of an ODF or MDF
- computation of the misorientation to mean for EBSD data
New Syntax for EBSD and grain variables
EBSD and grain variables can now be indexed by phase, region or grain / ebsd variables. Let us assume we have a two phase ebsd variable containing 'Fe' and 'Mg' then can restrict our dataset to the Fe - phase only by writing
ebsd('Fe')The same works with grains and also with more than one phase. Please have a look into the documentation for information how to index ebsd and grain variables.
Accordingly the following syntax is now depreciated.
calcODF(ebsd,'phase',2)
It should be replaced by
calcODF(ebsd('Fe'))Other Enhangments
- better import and export of pole figures, odfs and EBSD data
- automatic centering of a specimen with respect to its specimen symmetry
- download and import tensors from http://www.materialproperties.org/
- new interfaces for Rigaku, Siemens, Bruker and many other X-ray devices and formats
- support for rank three tensors, i.e, for piezo electricity tensors
- improved documentation
- many bug fixes
MTEX 3.1 - 03/2011
Tensor Arithmetics This release introduces tensor analysis into MTEX, this includes
- import of tensors via the import wizard
- basic tensor operations: multiplication, rotation, inversion
- advanced visualization
- computation of averaged tensors from EBSD data and ODFs
- computation of standard elasticity tensors like: Youngs modulus, linear compressibility, Christoffel tensor, elastic wave velocities
Other Enhancements
- support for different crystal reference frame conventions
- automatic conversion between different reference frames
- definition of crystal directions in direct and reciprocal space
- more predefines orientations: Cube, CubeND22, CubeND45, CubeRD, Goss, Copper, SR, Brass, PLage, QLage, ...
- improved EBSD and grain plots
- new and improved interfaces
- many bug fixes
MTEX 3.0 - 10/2010
Crystal Geometry
This release contains a completely redesigned crystal geometry engine which is thought to be much more intuitive and flexible. In particular, it introduces two new classes rotation and orientation which make it much easier to work with crystal orientations. Resulting features are
- no more need for quaternions
- support for Bunge, Roe, Matthies, Kocks, and Canova Euler angle convention
- a simple definition of fibres
- simply check whether two orientations are symmetrically equivalent
Other Enhancements
- automatic kernel selection in ODF estimation from EBSD data
- support for Bingham model ODFs
- estimation of Bingham parameters from EBSD data
- faster and more accurate EBSD simulation
- faster grain reconstruction
- improved documentation
- improved output
- MTEX is now compatible with NFFT 3.1.3
MTEX 2.0 - 10/2009
Grain Analysis for EBSD Data
MTEX is now able to partition spatial EBSD data into grains. This allows for the computation of various grain characteristics, as well as the computation and visualization of the grain boundaries and neighborhood relationships. Main features are:
- Grains statistics (area, diameter, mean orientation, ...)
- Missorientation analysis
- Interactive selection of grains by various criteria
- ODF-calculations for any subset of grains
- A large palette of plotting possibilities.
Visualization Improvements
- ODF fibre plot
- support for different x-axis alignment - plotx2north, plotx2east
- plot EBSD data with respect to arbitrary properties
- plot zero regions of ODFs and pole figures white
- pole figure contour plots
- color triangle for spatial EBSD plots
General Improvements
- ODF import / export
- rotate EBSD data
- Pole figure normalization
- improved interfaces and import wizard
- speed improvement of several side-functions as well as core-functions of @quaternions and spherical grids.
Incompatible Changes to Previous Versions
- The flags reduced and axial have been replaced by the flag antipodal
MTEX 1.2 - 05/2009
Improved EBSD import
- import-weighted EBSD (e.g. from odf modeling)
- new HKL and Chanel interfaces (.ang and .ctf files)
- import of multiple phases
- import of arbitrary properties as MAD, detection error, etc.
Improved EBSD plotting
- plot EBSD data in axis angle and Rodrigues space
- annotations in these spaces
- plot arbitrary properties as MAD, detection error, etc.
- better orientation colorcoding
- superpose odf, pole figure and EBSD plots
- better interpolation
General Improvements
- support for different crystal geometry setups
- faster and more accurate volume computation
- improved function modalorientation
- improved documentation
Incompatible Changes to Previous Versions
- The flag reduced has been replaced by the flag axial
MTEX 1.1 - 12/2008
Improved Import Wizzard
- Load CIF files to specify crystal geometry
- Import EBSD data with coordinates
- More options to specify the alignment of the specimen coordinate system
- support for popla *.epf files, *.plf files, and *.nja files
Improved Pole Figure Analysis
- Background correction and defocusing
- Outlier detection and elimination
Improved EBSD Data Support
- Spatial plot of EBSD data
- Modify EBSD data in the same way as pole figures
Improved Plotting
- GUI to modify plots more easily
- Annotate orientations into pole figure plots
- Annotate orientations into ODF sections
- Coordinate systems for ODF and pole figure plots
- More flexible and consistent option system
- Default plotting options like FontSize, Margin, ...
- Speed improvements
Bug Fixes
- ModalOrientation works now much better
- Plot (0,0) coordinate in ODF plot at upper left
- Fixed a bug in ODF estimation from EBSD data
MTEX 1.0 - 06/2008
New Installer Including Binaries for Windows, Linux, and Max OSX
- MTEX ships now with an automated installer and binaries for Windows, Linux, and Mac OSX. This makes it in unnecessary to install any additional library and to compile the toolbox. (Thanks to F. Bachmann, C. Randau, and F. Wobbe)
New ODF Class
- The new function FourierODF provides an easy way to define ODFs via their Fourier coefficients. In particular, MTEX allows now to calculate with those ODFs in the same manner as with any other ODFs.
New Interfaces
- New PoleFigure interface for xrdml data (F. Bachmann)
Improved Plotting
- Plot EBSD data and continuous ODFs into one plot
- Miller indices and specimen directions can now be plotted directly into pole figures or inverse pole figures.
- New plotting option north, south for spherical plots
- Improved colorbar handling
- Spherical grids
- More spherical projections
Incompatible Changes With Previous Releases
- The flag hemisphere in S2Grid has been replaced by north, south, and antipodal making it more consistent with the plotting routine.
Improved Documentation
MTEX comes now with over 500 help pages explaining the mathematical concepts, the philosophy behind MTEX and the syntax and usage of all 300 functions available in MTEX. Furthermore, you find numerous examples and tutorials on ODF estimation, data import, calculation of texture characteristics, ODF and pole figure plotting, etc.
Bug Fixes
- Fixed zero range method
- Fixed automatic ghost correction
- Fixed some loadPoleFigure issues
- Many other bug fixes.
MTEX 0.4 - 04/2008
Speed Improvements
- ODF reconstruction and PDF calculation are about 10 times faster now (thanks to the new NFFT 4.0 library)
- ODF plotting and the calculation of volume fractions, the texture index, the entropy and Fourier coefficients is about 100 times faster
New Support of EBSD Data Analysis
- Import EBSD data from arbitrary data formats.
- New class EBSD to store and manipulate with EBSD data.
- Plot pole figures and inverse pole figures from EBSD data.
- Recover ODFs from EBSD data via kernel density estimation.
- Estimate Fourier coefficients from EBSD data.
- Simulate EBSD data from ODFs.
- Export EBSD data.
New Functions
- fibreVolume calculates the volume fraction within a fibre.
- plotFourier plots the Fourier coefficients of an ODF.
- setcolorrange and the plotting option colorrange allow for consistent color coding for arbitrary plots.
- A colorbar can be added to any plots.
- mat2quat and quat2mat convert rotation matrices to quaternions and vice versa.
Incompatible Changes With Previous Releases
- New, more flexible syntax for the generation of S2Grids
- Slightly changed the syntax of unimodalODF and fibreODF.
- Default plotting options are set to {}, i.e. 'antipodal' has to add manually if desired
- Crystal symmetry triclinic is not called tricline anymore.
MTEX 0.3 - 10/2007
- new function fourier to calculate the Fourier coefficents of an arbitrary ODF
- new option ghost correction in function calcODF
- new option zero range in function calcODF
- new function loadEBSD to import EBSD data
- simplified syntax for the import of diffraction data
- new import wizard for pole figure data
- support of triclinic crystal symmetry with arbitrary angles between the axes
- default plotting options may now be specified in mtex_settings.m
- new plot option 3d for a three-dimensional spherical plot of pole figures
- contour levels may be specified explicitly in all plot functions plotodf,
and ODF.plotipdf.html,plotipdf - new plot option logarithmic
- many bugfixes
MTEX 0.2 - 07/2007
- new functions textureindex, entropy, volume
- creatly improved help
- improved installation
- new options for plotting routines for specific ODF sections
- many bugfixes
MTEX 0.1 - 03/2007
- initial release
| DocHelp 0.1 beta |