Analyzing Individual Grains
how to work with single grains
| On this page ... |
| Connection between grains and EBSD data |
| Visualize the misorientation within a grain |
| Testing on Bingham distribution for a single grain |
| Profiles through a single grain |
Connection between grains and EBSD data
As usual, we start by importing some EBSD data and computing grains
close all mtexdata forsterite plotx2east % consider only indexed data for grain segmentation ebsd = ebsd('indexed'); % compute the grains [grains,ebsd.grainId,ebsd.mis2mean] = calcGrains(ebsd);
The grains contain. We can access these data by
grain_selected = grains( grains.grainSize >= 1160) ebsd_selected = ebsd(grain_selected)
grain_selected = grain2d
Phase Grains Pixels Mineral Symmetry Crystal reference frame
1 32 62262 Forsterite mmm
boundary segments: 11070
triple points: 782
Properties: GOS, meanRotation
ebsd_selected = EBSD
Phase Orientations Mineral Color Symmetry Crystal reference frame
1 62262 (100%) Forsterite light blue mmm
Properties: bands, bc, bs, error, mad, x, y, grainId, mis2mean
Scan unit : um
A more convenient way to select grains in daily practice is by spatial coordinates.
grain_selected = grains(12000,3000)
grain_selected = grain2d
Phase Grains Pixels Mineral Symmetry Crystal reference frame
1 1 1208 Forsterite mmm
boundary segments: 238
triple points: 18
Id Phase Pixels GOS phi1 Phi phi2
640 1 1208 0.00806772 153 68 237
you can get the id of this grain by
grain_selected.id
ans = 640
let's look for the grain with the largest grain orientation spread
[~,id] = max(grains.GOS) grain_selected = grains(id)
id =
1856
grain_selected = grain2d
Phase Grains Pixels Mineral Symmetry Crystal reference frame
1 1 2614 Forsterite mmm
boundary segments: 458
triple points: 28
Id Phase Pixels GOS phi1 Phi phi2
1856 1 2614 0.170662 153 109 247
plot(grain_selected.boundary,'linewidth',2) hold on plot(ebsd(grain_selected)) hold off
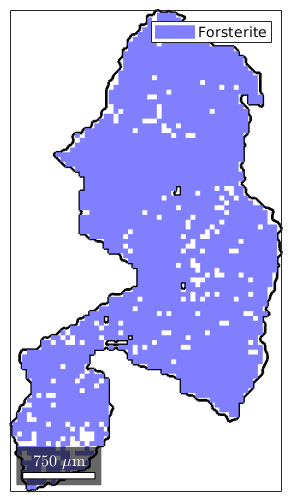
Visualize the misorientation within a grain
close plot(grain_selected.boundary,'linewidth',2) hold on plot(ebsd(grain_selected),ebsd(grain_selected).mis2mean.angle./degree) hold off mtexColorbar
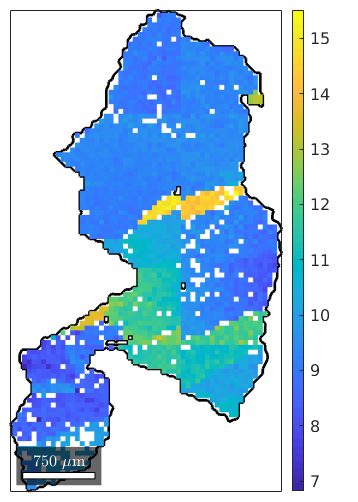
Testing on Bingham distribution for a single grain
Although the orientations of an individual grain are highly concentrated, they may vary in the shape. In particular, if the grain was deformed by some process, we are interested in quantifications.
cs = ebsd(grain_selected).CS;
ori = ebsd(grain_selected).orientations;
plotPDF(ori,[Miller(0,0,1,cs),Miller(0,1,1,cs),Miller(1,1,1,cs)],'antipodal')I'm plotting 1250 random orientations out of 2614 given orientations You can specify the the number points by the option "points". The option "all" ensures that all data are plotted
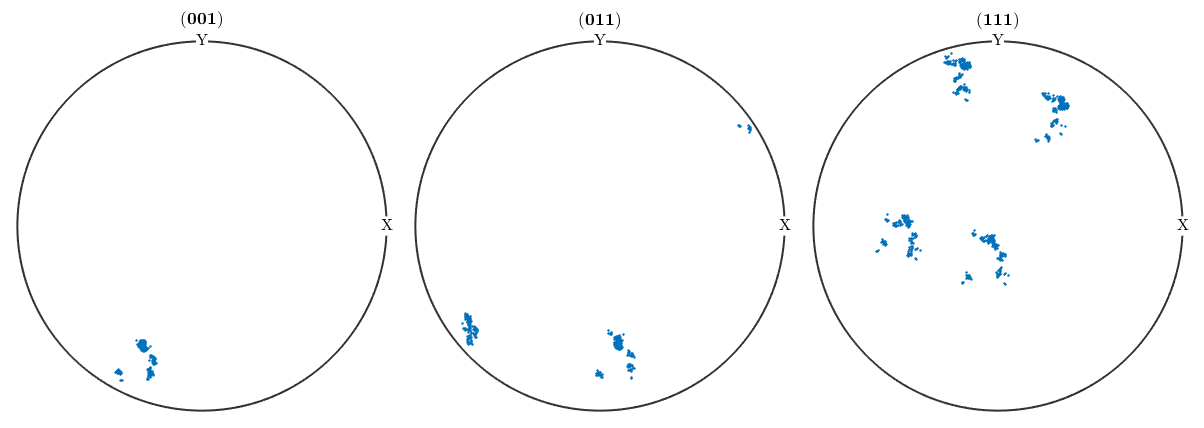
Testing on the distribution shows a gentle prolatness, nevertheless we would reject the hypothesis for some level of significance, since the distribution is highly concentrated and the numerical results vague.
calcBinghamODF(ori,'approximated')
ans = ODF
crystal symmetry : Forsterite (mmm)
specimen symmetry: 1
Bingham portion:
kappa: 0 4019.3061 4021.4833 4022.7958
weight: 1
T_spherical = bingham_test(ori,'spherical','approximated'); T_prolate = bingham_test(ori,'prolate', 'approximated'); T_oblate = bingham_test(ori,'oblate', 'approximated'); [T_spherical T_prolate T_oblate]
ans =
1 1 1
Profiles through a single grain
Sometimes, grains show large orientation difference when being deformed and then its of interest, to characterize the lattice rotation. One way is to order orientations along certain line segment and look at the profile.
We proceed by specifying such a line segment
close, plot(grain_selected.boundary,'linewidth',2) hold on, plot(ebsd(grain_selected),ebsd(grain_selected).orientations) % line segment lineSec = [18826 6438; 18089 10599]; line(lineSec(:,1),lineSec(:,2),'linewidth',2)
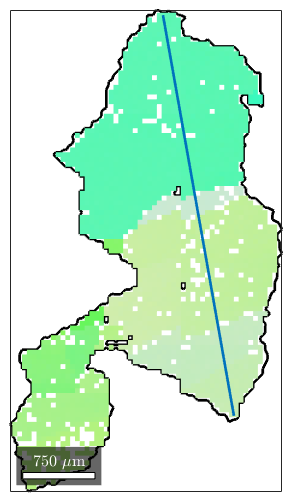
The command spatialProfile restricts the EBSD data to this line
ebsd_line = spatialProfile(ebsd(grain_selected),lineSec);
Next, we plot the misorientation angle to the first point of the line as well as the orientation gradient
close all % close previous plots % misorientation angle to the first orientation on the line plot(ebsd_line.y,... angle(ebsd_line(1).orientations,ebsd_line.orientations)/degree) % misorientation gradient hold all plot(0.5*(ebsd_line.y(1:end-1)+ebsd_line.y(2:end)),... angle(ebsd_line(1:end-1).orientations,ebsd_line(2:end).orientations)/degree) hold off xlabel('y'); ylabel('misorientation angle in degree') legend('to reference orientation','orientation gradient')
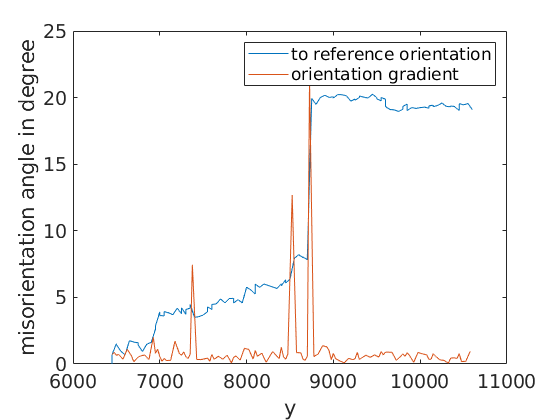
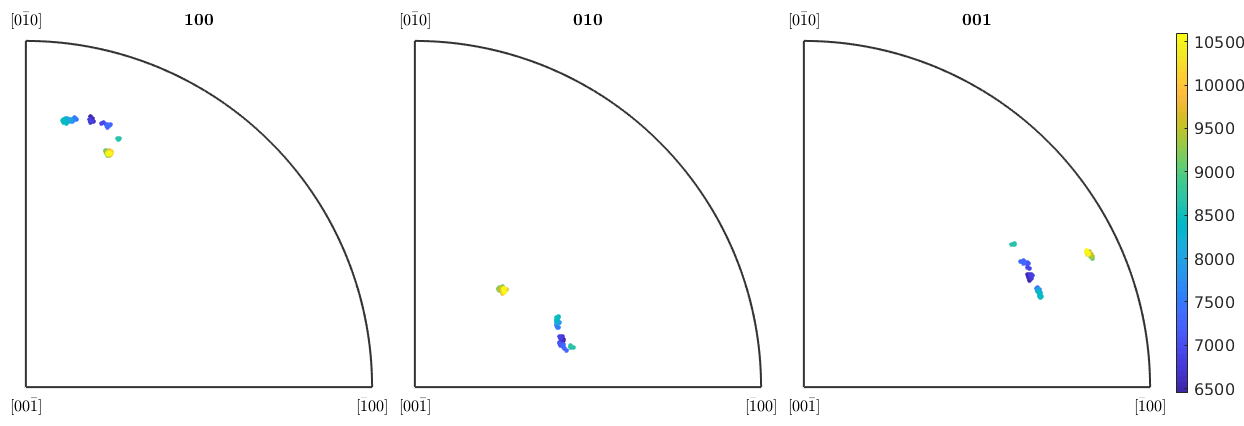
We can also plot the orientations along this line into inverse pole figures and colorize them according to their y-coordinate
close, plotIPDF(ebsd_line.orientations,[xvector,yvector,zvector],... 'property',ebsd_line.y,'markersize',3,'antipodal') mtexColorbar
| DocHelp 0.1 beta |