S2AxisFieldHarmonic

S2AxisFieldharmonic handles axis fields on the sphere. Axis can be understood as three-dimensional vectors without direction or length.

Defining a S2AxisFieldHarmonic

Visualization

Complete Function list

S2AxisFieldHarmonic handles functions of the form

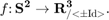
Defining a S2AxisFieldHarmonic

Definition via function values

At first you need some vertices

nodes = equispacedS2Grid('points', 1e5);
nodes = nodes(:);

Next you define function values for the vertices

y = vector3d(sin(5*nodes.x), 1, nodes.y, 'antipodal');

Now the actual command to get sAF1 of type S2AxisFieldHarmonic

sAF1 = S2AxisFieldHarmonic.approximation(nodes, y)

 
sAF1 = S2AxisFieldHarmonic  
 bandwidth: 224

Definition via function handle

If you have a function handle for the function you could create a S2AxisFieldHarmonic via quadrature. At first lets define a function handle which takes vector3d as an argument and returns antipodal vector3d:

f = @(v) vector3d(v.x, v.y, 0*v.x, 'antipodal');

Now you can call the quadrature command to get sAF2 of type S2AxisFieldHarmonic

sAF2 = S2AxisFieldHarmonic.quadrature(@(v) f(v))

 
sAF2 = S2AxisFieldHarmonic  
 bandwidth: 128

Visualization

the default plot-command

plot(sAF1);

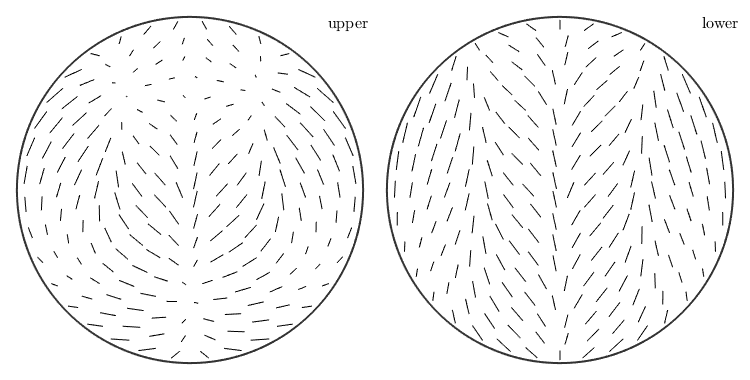
same as quiver(sAF1)

3D plot of a sphere with the axis on itself

clf;
quiver3(sAF2);