Twinning Analysis
Explains how to detect and quantify twin boundaries
Data import and grain detection
Lets import some Magnesium data that are full of grains and segment grain within the data set.
% load some example data mtexdata twins % segment grains [grains,ebsd.grainId,ebsd.mis2mean] = calcGrains(ebsd('indexed'),'angle',5*degree); % remove two pixel grains ebsd(grains(grains.grainSize<=2)) = []; [grains,ebsd.grainId,ebsd.mis2mean] = calcGrains(ebsd('indexed'),'angle',5*degree); % smooth them grains = grains.smooth(5); % visualize the grains plot(grains,grains.meanOrientation) % store crystal symmetry of Magnesium CS = grains.CS;
I'm going to colorize the orientation data with the standard MTEX colorkey. To view the colorkey do: colorKey = ipfColorKey(ori_variable_name) plot(colorKey)
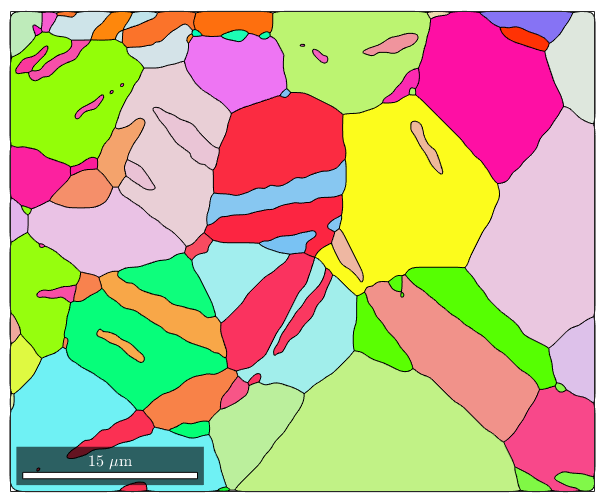
Now we can extract from the grains its boundary and save it to a separate variable
gB = grains.boundary
gB = grainBoundary
Segments mineral 1 mineral 2
600 notIndexed Magnesium
3164 Magnesium Magnesium
The output tells us that we have 3219 Magnesium to Magnesium boundary segments and 606 boundary segements where the grains are cut by the scanning boundary. To restrict the grain boundaries to a specific phase transistion you shall do
gB_MgMg = gB('Magnesium','Magnesium')
gB_MgMg = grainBoundary
Segments mineral 1 mineral 2
3164 Magnesium Magnesium
Properties of grain boundaries
A variable of type grain boundary contains the following properties
- misorientation
- direction
- segLength
These can be used to colorize the grain boundaries. By the following command, we plot the grain boundaries colorized by the misorientation angle
plot(gB_MgMg,gB_MgMg.misorientation.angle./degree,'linewidth',2)
mtexColorbar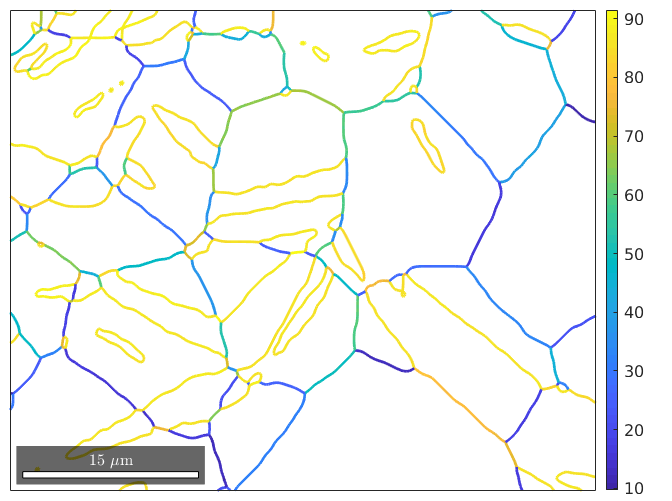
We observe many grain boundaries with a large misorientation angle of about 86 degrees. Those grain boundaries are most likely twin boundaries. To detect them more precisely we define first the twinning as a misorientation, which is reported in literature by (1,1,-2,0) parallel to (2,-1,-1,0) and (-1,0,1,1) parallel to (1,0,-1,1). In MTEX it is defined by
twinning = orientation.map(Miller(1,1,-2,0,CS),Miller(2,-1,-1,0,CS),...
Miller(-1,0,1,1,CS),Miller(-1,1,0,1,CS))twinning = misorientation size: 1 x 1 crystal symmetry : Magnesium (6/mmm, X||a*, Y||b, Z||c*) crystal symmetry : Magnesium (6/mmm, X||a*, Y||b, Z||c*) Bunge Euler angles in degree phi1 Phi phi2 Inv. 300 0 0 0
The followin lines show that the twinning is actually a rotation about axis (-2110) and angle 86.3 degree
% the rotational axis round(twinning.axis) % the rotational angle twinning.angle / degree
ans = Miller
size: 1 x 1
mineral: Magnesium (622, X||a*, Y||b, Z||c*)
h 1
k 0
i -1
l 0
ans =
0
Next, we check for each boundary segment whether it is a twinning boundary, i.e., whether boundary misorientation is close to the twinning.
% restrict to twinnings with threshold 5 degree isTwinning = angle(gB_MgMg.misorientation,twinning) < 5*degree; twinBoundary = gB_MgMg(isTwinning) % plot the twinning boundaries plot(grains,grains.meanOrientation) %plot(ebsd('indexed'),ebsd('indexed').orientations) hold on %plot(gB_MgMg,angle(gB_MgMg.misorientation,twinning),'linewidth',4) plot(twinBoundary,'linecolor','w','linewidth',2,'displayName','twin boundary') hold off
twinBoundary = grainBoundary grain boundary is empty! I'm going to colorize the orientation data with the standard MTEX colorkey. To view the colorkey do: colorKey = ipfColorKey(ori_variable_name) plot(colorKey)
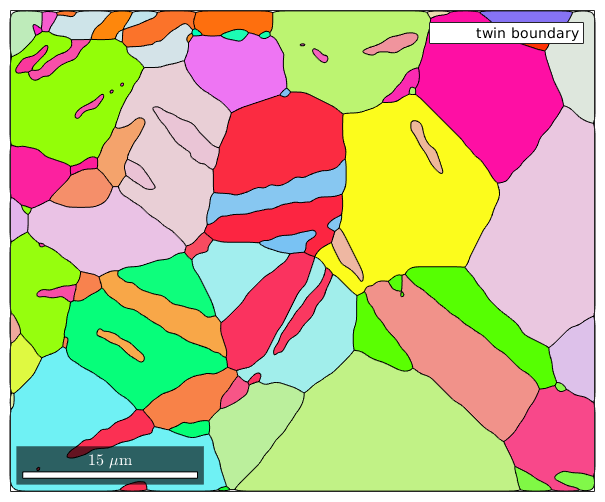
Merge twins along twin boundaries
Grains that have a common twin boundary are assumed to inherite from one common grain. To reconstruct those initial grains we merge grains together which have a common twin boundary. This is done by the command merge.
[mergedGrains,parentId] = merge(grains,twinBoundary); % plot the merged grains %plot(ebsd,ebsd.orientations) hold on plot(mergedGrains.boundary,'linecolor','k','linewidth',2.5,'linestyle','-',... 'displayName','merged grains') hold off
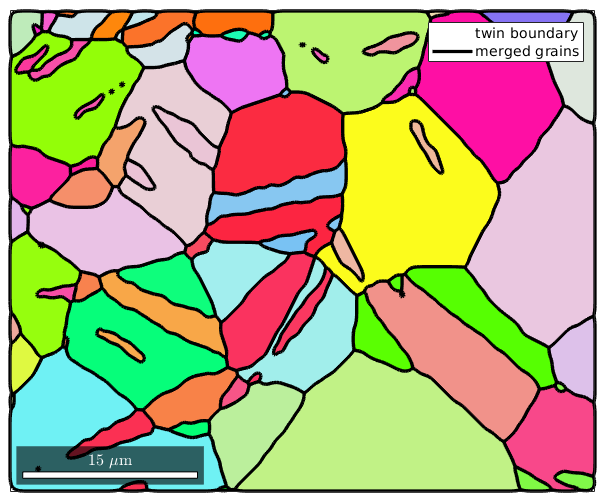
Grain relationships
The second output argument paraentId of merge is a list with the same size as grains which indicates for each grain into which common grain it has been merged. The id of the common grain is usually different from the ids of the merged grains and can be found by
mergedGrains(16).id
ans =
16
Hence, we can find all childs of grain 16 by
childs = grains(parentId == mergedGrains(16).id)
childs = grain2d
Phase Grains Pixels Mineral Symmetry Crystal reference frame
1 1 1427 Magnesium 6/mmm X||a*, Y||b, Z||c*
boundary segments: 286
triple points: 9
Id Phase Pixels GOS phi1 Phi phi2
16 1 1427 0.01101 4 81 195
Calculate the twinned area
We can also answer the question about the relative area of these initial grains that have undergone twinning to total area.
twinId = unique(gB_MgMg(isTwinning).grainId);
% compute the area fraction
sum(area(grains(twinId))) / sum(area(grains)) * 100ans =
0
Setting Up the EBSD Data for the Merged Grains
Note that the Id's of the merged grains does not fit the grainIds stored in the initial ebsd variable. As a consequence, the following command will not give the right result
plot(mergedGrains(16).boundary,'linewidth',2) hold on plot(ebsd(mergedGrains(16)),ebsd(mergedGrains(16)).orientations) hold off
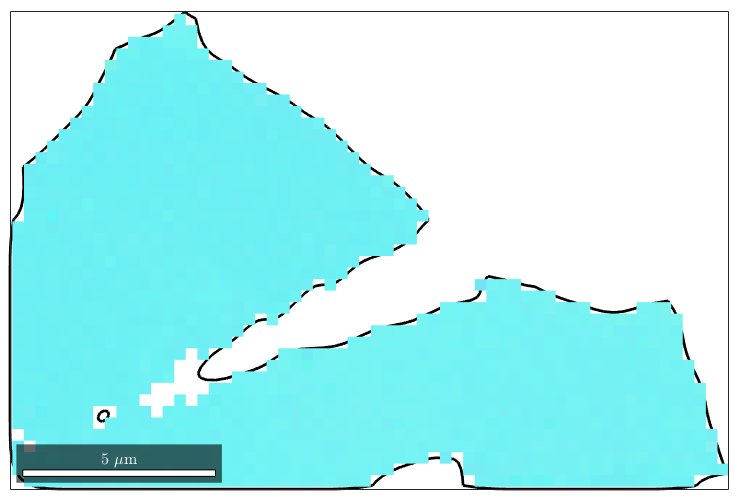
In order to update the grainId in the ebsd variable to the merged grains, we proceed as follows.
% copy ebsd data into a new variable to not change the old data ebsd_merged = ebsd; % update the grainIds to the parentIds ebsd_merged('indexed').grainId = parentId(ebsd('indexed').grainId)
ebsd_merged = EBSD
Phase Orientations Mineral Color Symmetry Crystal reference frame
0 46 (0.2%) notIndexed
1 22794 (100%) Magnesium light blue 6/mmm X||a*, Y||b, Z||c*
Properties: bands, bc, bs, error, mad, x, y, grainId, mis2mean
Scan unit : um
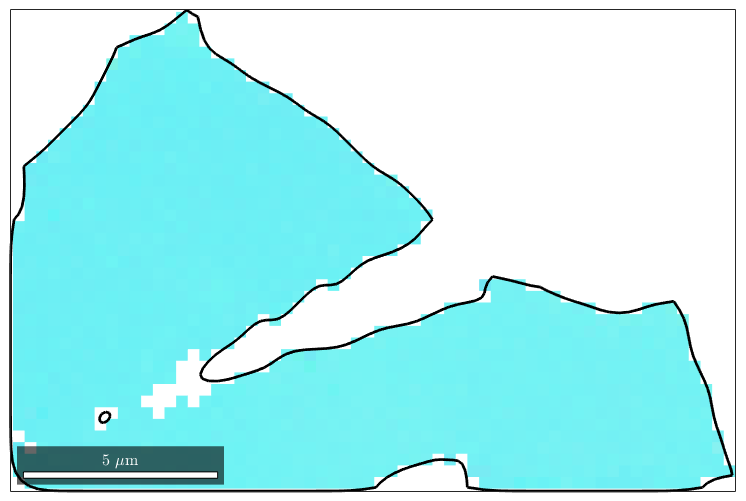
Now the variable ebsd_merged can be indexed by the merged grains, i.e.
plot(ebsd_merged(mergedGrains(16)),ebsd_merged(mergedGrains(16)).orientations) hold on plot(mergedGrains(16).boundary,'linewidth',2) hold off
| DocHelp 0.1 beta |