Slip Transmission
How to analyze slip transmission at grain boundaries
| On this page ... |
| Import Titanium data |
| Schmid Factor |
| Resolved shear stress |
| Compatibility of slip systems |
| Plot m' in misorientation space |
Import Titanium data
From Mercier D. - MTEX 2016 Workshop - TU Chemnitz (Germany) Calculation and plot on GBs of m' parameter Dataset from Mercier D. - cp-Ti (alpha phase - hcp)
mtexdata titanium % compute grains [grains, ebsd.grainId] = calcGrains(ebsd('indexed')); % make them a bit nicer grains = smooth(grains); % extract inner phase grain boundaries gB = grains.boundary('indexed'); plot(ebsd,ebsd.orientations) hold on plot(grains.boundary) hold off

Schmid Factor
% consider Basal slip sSBasal = slipSystem.basal(ebsd.CS) % and all symmetrically equivalent variants sSBasal = sSBasal.symmetrise; % compute Schmid factor for all slip systems SF = sSBasal.SchmidFactor(inv(grains.meanOrientation) * xvector); % find the maximum Schmidt factor [SF,id] = max(SF,[],2); % and plot it for each grain plot(grains,SF) mtexColorbar
sSBasal = slipSystem mineral: Titanium (Alpha) (622, X||a, Y||b*, Z||c) size: 1 x 1 U V T W | H K I L CRSS 1 1 -2 0 0 0 0 1 1
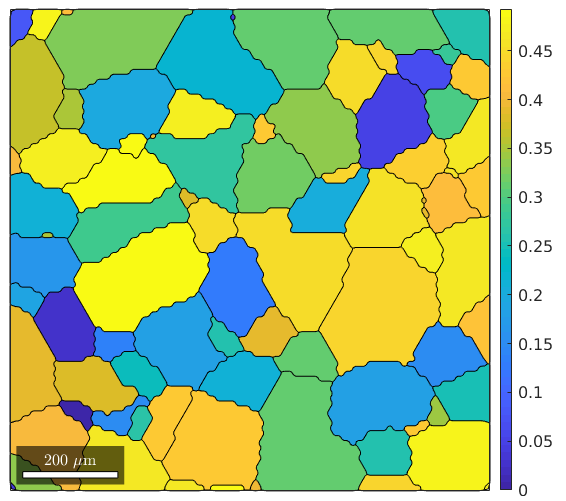
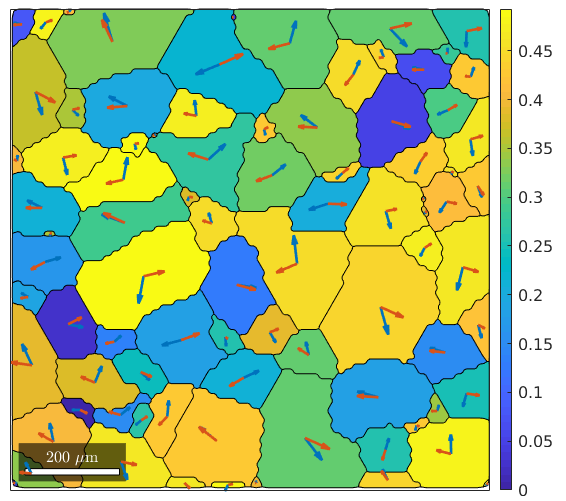
The variable id contains now for each grain the id of the slip system with the largest Schmidt factor. In order to visualize it, we first rotate for each grain the slip system with largest Schmid factor in specimen coordinates
sSGrain = grains.meanOrientation .* sSBasal(id) % and then plot the plane normal and the Burgers vectors into the centers % of the grains hold on quiver(grains,cross(sSGrain.n,zvector),'displayName','slip plane') hold on quiver(grains,sSGrain.b,'displayName','slip direction') hold off
sSGrain = slipSystem CRSS: 1 size: 85 x 1
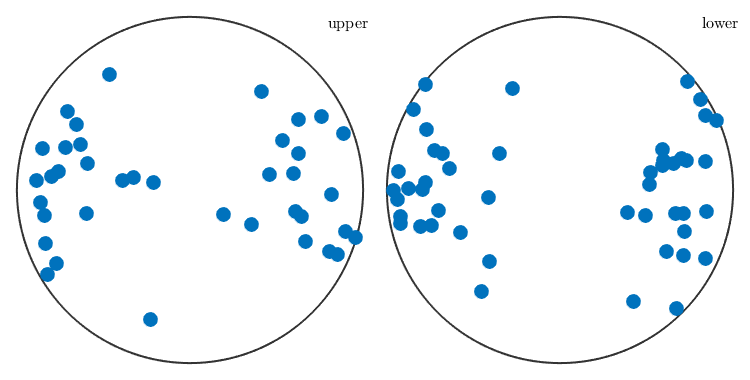
We may also analyse the distribution of the slip directions in a pole figure plot
plot(sSGrain.b)
The same as a contour plot. We see a clear trend towards the east.
plot(sSGrain.b,'contourf')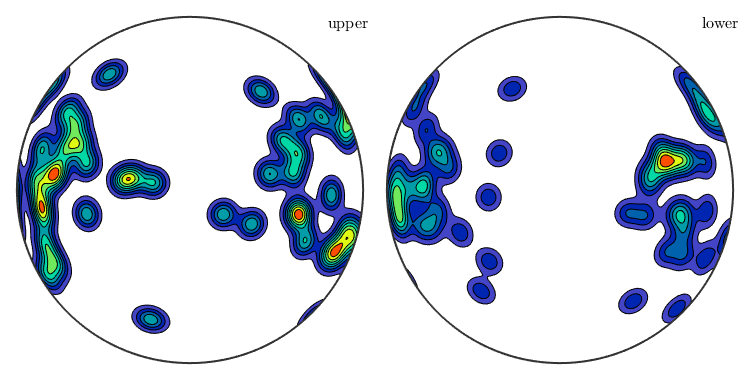
Resolved shear stress
We could do the same as above with a more general stress tensor. However, the result is a bit different. TODO: why the directions do not point towards east???
% more general syntax for the same stress tensor sigma = stressTensor.uniaxial(xvector); % compute Schmid factor for all slip systems SF = sSBasal.SchmidFactor(inv(grains.meanOrientation) * sigma); % find the maximum Schmidt factor [SF,id] = max(SF,[],2); % plot the Schmid factor plot(grains,SF) mtexColorbar % active slip system in specimen coordinates sSGrain = grains.meanOrientation .* sSBasal(id) % and plot then the plance normal and the Burgers vectors into the centers % of the grains hold on quiver(grains,cross(sSGrain.n,zvector),'displayName','slip plane') hold on quiver(grains,sSGrain.b,'displayName','slip direction') hold off
sSGrain = slipSystem CRSS: 1 size: 85 x 1
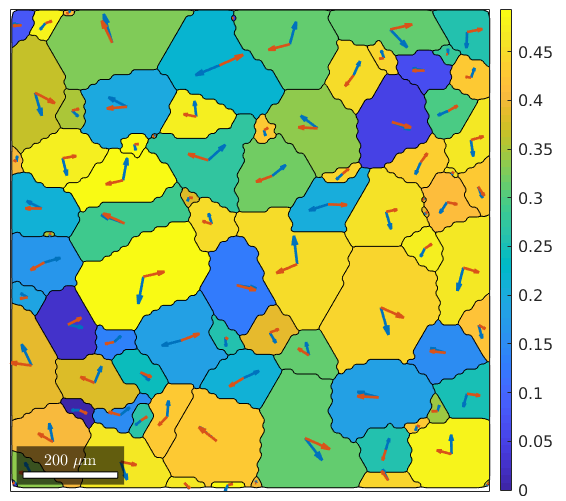
Compatibility of slip systems
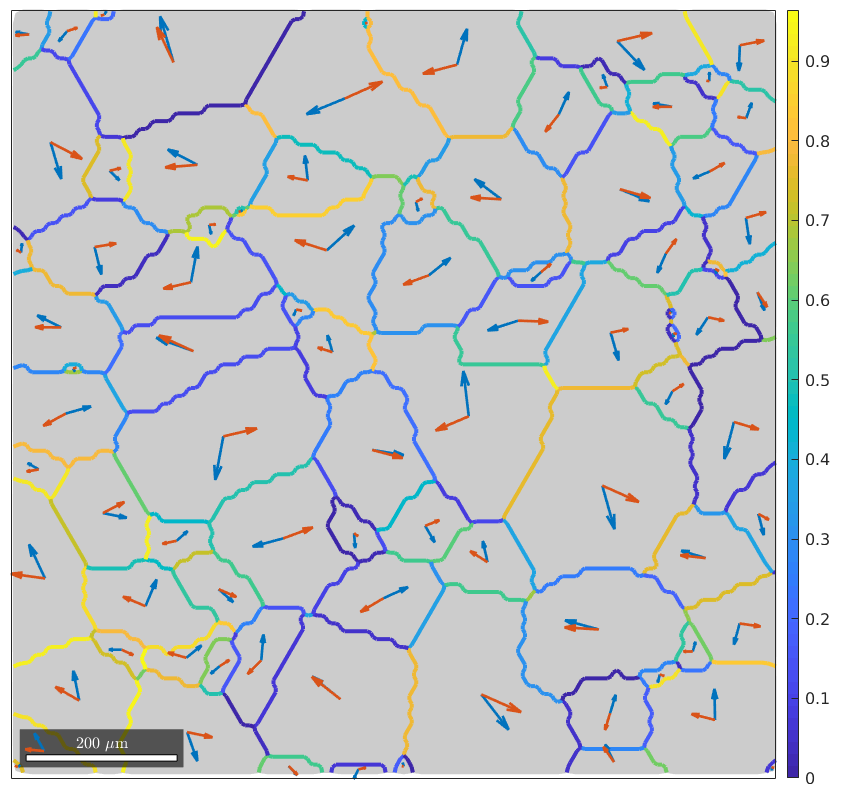
Next, we want to analyze, how much geometrically compatible the slip systems with highest Schmid factor are at the grain boundaries
% some background plot(grains,'FaceColor',0.8*[1 1 1],'figSize','large') % compute m' id = gB.grainId; mP = mPrime(sSGrain(id(:,1)),sSGrain(id(:,2))); % plot m' along the grain boundaries hold on plot(gB,mP,'linewidth',3) mtexColorbar % and plot then the plance normal and the Burgers vectors into the centers % of the grains hold on quiver(grains,cross(sSGrain.n,zvector),'displayName','slip plane') hold on quiver(grains,sSGrain.b,'displayName','slip direction') hold off
Plot m' in misorientation space
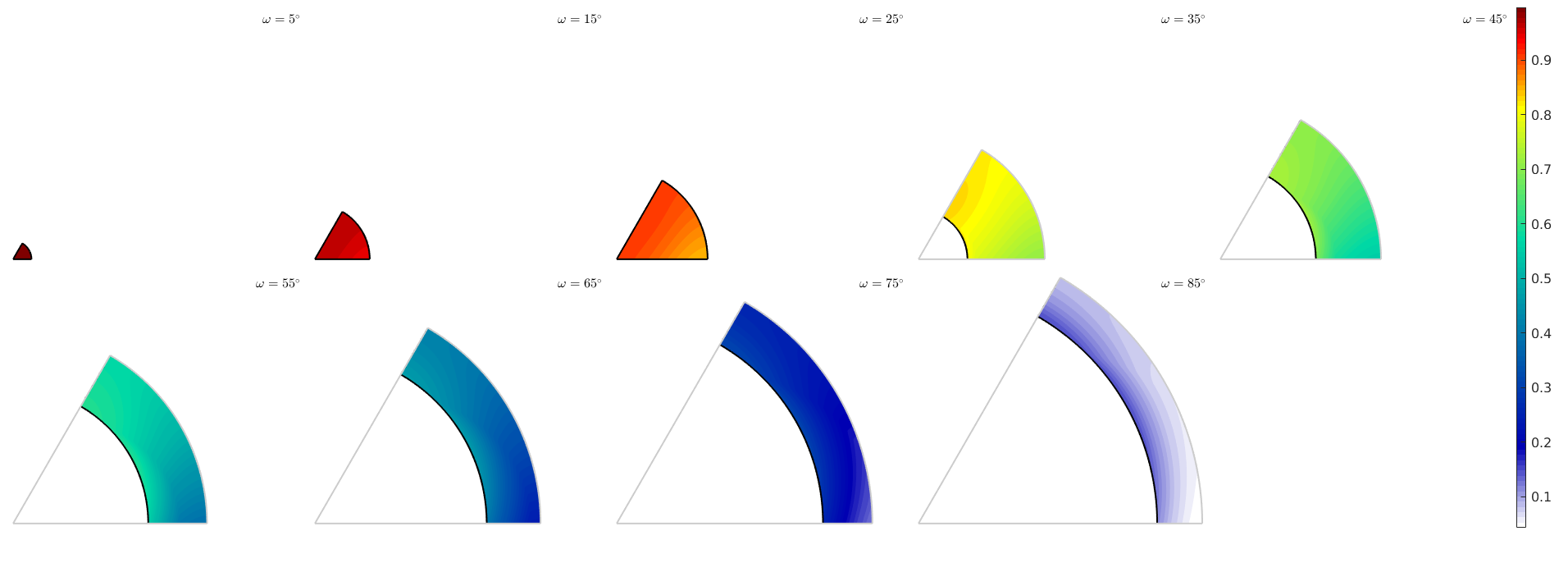
Since m' depends on the misorientation only why may plot it directly in misorientation space
% set up an axis angle plot sP = axisAngleSections(sSBasal.CS,sSBasal.CS); % generate a grid of misorientations moriGrid = sP.makeGrid; % compute mPrime for all misorientations sSBasal = slipSystem.basal(ebsd.CS); mP = max(mPrime(sSBasal,moriGrid*sSBasal.symmetrise),[],2); % plot mPrime sP.plot(mP,'smooth') mtexColorbar
| DocHelp 0.1 beta |