Average Material Tensors
how to calculate average material tensors from ODF and EBSD data
MTEX offers several ways to compute average material tensors from ODFs or EBSD data.
| On this page ... |
| Import EBSD Data |
| Data Correction |
| Define Elastic Stiffness Tensors for Glaucophane and Epidote |
| The Average Tensor from EBSD Data |
| ODF Estimation |
| The Average Tensor from an ODF |
set up a nice colormap
setMTEXpref('defaultColorMap',blue2redColorMap);
Import EBSD Data
We start by importing some EBSD data of Glaucophane and Epidote.
ebsd = EBSD.load([mtexDataPath '/EBSD/data.ctf'],... 'convertEuler2SpatialReferenceFrame')
ebsd = EBSD
Phase Orientations Mineral Color Symmetry Crystal reference frame
0 28015 (56%) notIndexed
1 13855 (28%) Glaucophane light blue 12/m1 X||a*, Y||b*, Z||c
2 4603 (9.2%) Epidote light green 12/m1 X||a*, Y||b*, Z||c
3 3213 (6.4%) Pyrope light red m-3m
4 295 (0.59%) omphacite cyan 12/m1 X||a*, Y||b*, Z||c
Properties: bands, bc, bs, error, mad, x, y
Scan unit : um
Let's visualize a subset of the data
plot(ebsd(inpolygon(ebsd,[2000 0 1400 375])))
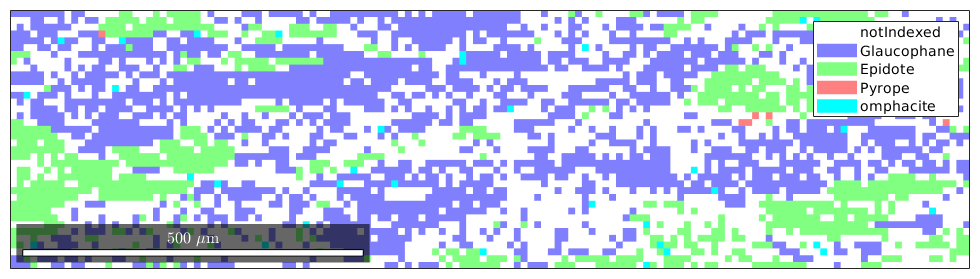
Data Correction
next, we correct the data by excluding orientations with large MAD value
% define maximum acceptable MAD value MAD_MAXIMUM= 1.3; % eliminate all meassurements with MAD larger than MAD_MAXIMUM ebsd(ebsd.mad >MAD_MAXIMUM) = [] plot(ebsd(inpolygon(ebsd,[2000 0 1400 375])))
ebsd = EBSD
Phase Orientations Mineral Color Symmetry Crystal reference frame
0 28015 (56%) notIndexed
1 13779 (28%) Glaucophane light blue 12/m1 X||a*, Y||b*, Z||c
2 4510 (9.1%) Epidote light green 12/m1 X||a*, Y||b*, Z||c
3 3212 (6.5%) Pyrope light red m-3m
4 218 (0.44%) omphacite cyan 12/m1 X||a*, Y||b*, Z||c
Properties: bands, bc, bs, error, mad, x, y
Scan unit : um
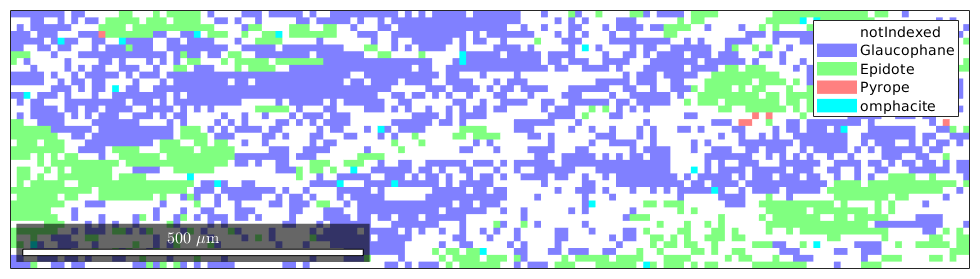
Define Elastic Stiffness Tensors for Glaucophane and Epidote
Glaucophane elastic stiffness (Cij) Tensor in GPa Bezacier, L., Reynard, B., Bass, J.D., Wang, J., and Mainprice, D. (2010) Elasticity of glaucophane and seismic properties of high-pressure low-temperature oceanic rocks in subduction zones. Tectonophysics, 494, 201-210.
% define the tensor coefficients MGlaucophane =.... [[122.28 45.69 37.24 0.00 2.35 0.00];... [ 45.69 231.50 74.91 0.00 -4.78 0.00];... [ 37.24 74.91 254.57 0.00 -23.74 0.00];... [ 0.00 0.00 0.00 79.67 0.00 8.89];... [ 2.35 -4.78 -23.74 0.00 52.82 0.00];... [ 0.00 0.00 0.00 8.89 0.00 51.24]]; % define the reference frame csGlaucophane = crystalSymmetry('2/m',[9.5334,17.7347,5.3008],... [90.00,103.597,90.00]*degree,'X||a*','Z||c','mineral','Glaucophane'); % define the tensor CGlaucophane = stiffnessTensor(MGlaucophane,csGlaucophane)
CGlaucophane = stiffnessTensor
unit : GPa
rank : 4 (3 x 3 x 3 x 3)
mineral: Glaucophane (12/m1, X||a*, Y||b*, Z||c)
tensor in Voigt matrix representation:
122.28 45.69 37.24 0 2.35 0
45.69 231.5 74.91 0 -4.78 0
37.24 74.91 254.57 0 -23.74 0
0 0 0 79.67 0 8.89
2.35 -4.78 -23.74 0 52.82 0
0 0 0 8.89 0 51.24
Epidote elastic stiffness (Cij) Tensor in GPa Aleksandrov, K.S., Alchikov, U.V., Belikov, B.P., Zaslavskii, B.I. and Krupnyi, A.I.: 1974 'Velocities of elastic waves in minerals at atmospheric pressure and increasing the precision of elastic constants by means of EVM (in Russian)', Izv. Acad. Sci. USSR, Geol. Ser.10, 15-24.
% define the tensor coefficients MEpidote =.... [[211.50 65.60 43.20 0.00 -6.50 0.00];... [ 65.60 239.00 43.60 0.00 -10.40 0.00];... [ 43.20 43.60 202.10 0.00 -20.00 0.00];... [ 0.00 0.00 0.00 39.10 0.00 -2.30];... [ -6.50 -10.40 -20.00 0.00 43.40 0.00];... [ 0.00 0.00 0.00 -2.30 0.00 79.50]]; % define the reference frame csEpidote= crystalSymmetry('2/m',[8.8877,5.6275,10.1517],... [90.00,115.383,90.00]*degree,'X||a*','Z||c','mineral','Epidote'); % define the tensor CEpidote = stiffnessTensor(MEpidote,csEpidote)
CEpidote = stiffnessTensor
unit : GPa
rank : 4 (3 x 3 x 3 x 3)
mineral: Epidote (12/m1, X||a*, Y||b*, Z||c)
tensor in Voigt matrix representation:
211.5 65.6 43.2 0 -6.5 0
65.6 239 43.6 0 -10.4 0
43.2 43.6 202.1 0 -20 0
0 0 0 39.1 0 -2.3
-6.5 -10.4 -20 0 43.4 0
0 0 0 -2.3 0 79.5
The Average Tensor from EBSD Data
The Voigt, Reuss, and Hill averages for all phases are computed by
[CVoigt,CReuss,CHill] = calcTensor(ebsd({'Epidote','Glaucophane'}),CGlaucophane,CEpidote)CVoigt = stiffnessTensor unit: GPa rank: 4 (3 x 3 x 3 x 3) tensor in Voigt matrix representation: 216.77 52.91 67.88 -1.96 -4.2 5.19 52.91 158.05 54.54 -3.39 -0.46 2.47 67.88 54.54 206.78 -7.29 -2.37 1.72 -1.96 -3.39 -7.29 60.88 2.2 -0.82 -4.2 -0.46 -2.37 2.2 75.31 -1.58 5.19 2.47 1.72 -0.82 -1.58 61.01 CReuss = stiffnessTensor unit: GPa rank: 4 (3 x 3 x 3 x 3) tensor in Voigt matrix representation: 197.74 48.59 60.64 -1.71 -4.26 4.72 48.59 145.04 49.96 -2.86 -0.38 2.02 60.64 49.96 188.42 -6.3 -2.2 1.41 -1.71 -2.86 -6.3 55.31 2.18 -0.6 -4.26 -0.38 -2.2 2.18 69.75 -1.61 4.72 2.02 1.41 -0.6 -1.61 55.39 CHill = stiffnessTensor unit: GPa rank: 4 (3 x 3 x 3 x 3) tensor in Voigt matrix representation: 207.25 50.75 64.26 -1.83 -4.23 4.96 50.75 151.55 52.25 -3.13 -0.42 2.24 64.26 52.25 197.6 -6.79 -2.28 1.57 -1.83 -3.13 -6.79 58.09 2.19 -0.71 -4.23 -0.42 -2.28 2.19 72.53 -1.59 4.96 2.24 1.57 -0.71 -1.59 58.2
for a single phase the syntax is
[CVoigtEpidote,CReussEpidote,CHillEpidote] = calcTensor(ebsd('Epidote'),CEpidote)
CVoigtEpidote = stiffnessTensor
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
210.22 56.37 68.44 -1.49 -2.64 4.27
56.37 177.4 57.14 0.01 0.75 -0.11
68.44 57.14 205.87 -1.8 -0.08 1.24
-1.49 0.01 -1.8 59.21 1.55 0.53
-2.64 0.75 -0.08 1.55 72.83 -0.79
4.27 -0.11 1.24 0.53 -0.79 59.51
CReussEpidote = stiffnessTensor
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
197.04 57.67 69.57 -1.69 -2.32 4.16
57.67 161.32 59.28 -0.11 1.21 0.03
69.57 59.28 193.44 -1.78 0.78 1.05
-1.69 -0.11 -1.78 51.7 1.69 0.44
-2.32 1.21 0.78 1.69 66.46 -0.71
4.16 0.03 1.05 0.44 -0.71 51.98
CHillEpidote = stiffnessTensor
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
203.63 57.02 69 -1.59 -2.48 4.22
57.02 169.36 58.21 -0.05 0.98 -0.04
69 58.21 199.66 -1.79 0.35 1.14
-1.59 -0.05 -1.79 55.46 1.62 0.48
-2.48 0.98 0.35 1.62 69.65 -0.75
4.22 -0.04 1.14 0.48 -0.75 55.74
ODF Estimation
Next, we estimate an ODF for the Epidote phase
odfEpidote = calcODF(ebsd('Epidote').orientations,'halfwidth',10*degree)
odfEpidote = ODF
crystal symmetry : Epidote (12/m1, X||a*, Y||b*, Z||c)
specimen symmetry: 1
Harmonic portion:
degree: 25
weight: 1
The Average Tensor from an ODF
The Voigt, Reuss, and Hill averages for the above ODF are computed by
[CVoigtEpidote, CReussEpidote, CHillEpidote] = ... calcTensor(odfEpidote,CEpidote) % set back the colormap setMTEXpref('defaultColorMap',WhiteJetColorMap);
CVoigtEpidote = stiffnessTensor
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
208.94 57.35 67.73 -1.31 -2.25 3.75
57.35 177.36 57.99 -0.15 0.58 0.23
67.73 57.99 204.96 -1.61 -0.18 1.08
-1.31 -0.15 -1.61 60.13 1.37 0.37
-2.25 0.58 -0.18 1.37 72.05 -0.66
3.75 0.23 1.08 0.37 -0.66 60.49
CReussEpidote = stiffnessTensor
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
195.18 58.63 68.58 -1.49 -1.82 3.66
58.63 161.47 60 -0.24 0.99 0.3
68.58 60 192.09 -1.6 0.62 0.87
-1.49 -0.24 -1.6 52.4 1.49 0.35
-1.82 0.99 0.62 1.49 65.38 -0.57
3.66 0.3 0.87 0.35 -0.57 52.74
CHillEpidote = stiffnessTensor
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
202.06 57.99 68.15 -1.4 -2.03 3.7
57.99 169.42 58.99 -0.19 0.79 0.27
68.15 58.99 198.53 -1.6 0.22 0.97
-1.4 -0.19 -1.6 56.27 1.43 0.36
-2.03 0.79 0.22 1.43 68.71 -0.62
3.7 0.27 0.97 0.36 -0.62 56.61
| DocHelp 0.1 beta |